题目内容
设向量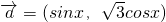 ,
,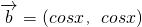 .
.
(1)若 (0<x<
(0<x< ),求tanx的值;
),求tanx的值;
(2)求函数f(x)= 的最小正周期和函数在
的最小正周期和函数在 的最大值及相应x的值.
的最大值及相应x的值.
解:(1)∵向量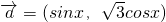 ,
,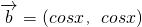 ,
, ,∴sinxcosx-
,∴sinxcosx- cos2x=0.
cos2x=0.
∵0<x< ,∴sinx-
,∴sinx- cosx=0,tanx=
cosx=0,tanx=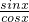 =
= .
.
(2)函数f(x)= =sinxcosx-
=sinxcosx- cos2x=
cos2x=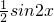 +
+ cos2x+
cos2x+
=sin(2x+ )+
)+ ,故它的最小正周期为
,故它的最小正周期为 =π.
=π.
再由 ,可得 2x+
,可得 2x+ ∈(
∈( ,
, ),
),
故当 2x+ =
= 时,函数取得最大值为
时,函数取得最大值为 ,此时,x=
,此时,x= .
.
分析:(1)利用两个向量平行的性质可得 sinxcosx- cos2x=0,再由 0<x<
cos2x=0,再由 0<x< ,以及同角三角函数的基本关系求得tanx的值.
,以及同角三角函数的基本关系求得tanx的值.
(2)利用两个向量的数量积公式以及两角和差的正弦公式求得f(x)=sin(2x+ )+
)+ ,由此求得它的最小正周期.再根据正弦函数的定义域和值域,求得函数的最大值.
,由此求得它的最小正周期.再根据正弦函数的定义域和值域,求得函数的最大值.
点评:本题主要考查两个向量平行的性质,两个向量的数量积公式,两角和差的正弦公式,同角三角函数的基本关系,正弦函数的定义域和值域,属于中档题.
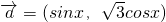 ,
,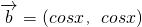 ,
, ,∴sinxcosx-
,∴sinxcosx- cos2x=0.
cos2x=0.∵0<x<
 ,∴sinx-
,∴sinx- cosx=0,tanx=
cosx=0,tanx=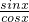 =
= .
.(2)函数f(x)=
 =sinxcosx-
=sinxcosx- cos2x=
cos2x=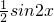 +
+ cos2x+
cos2x+
=sin(2x+
 )+
)+ ,故它的最小正周期为
,故它的最小正周期为 =π.
=π.再由
 ,可得 2x+
,可得 2x+ ∈(
∈( ,
, ),
),故当 2x+
 =
= 时,函数取得最大值为
时,函数取得最大值为 ,此时,x=
,此时,x= .
.分析:(1)利用两个向量平行的性质可得 sinxcosx-
 cos2x=0,再由 0<x<
cos2x=0,再由 0<x< ,以及同角三角函数的基本关系求得tanx的值.
,以及同角三角函数的基本关系求得tanx的值.(2)利用两个向量的数量积公式以及两角和差的正弦公式求得f(x)=sin(2x+
 )+
)+ ,由此求得它的最小正周期.再根据正弦函数的定义域和值域,求得函数的最大值.
,由此求得它的最小正周期.再根据正弦函数的定义域和值域,求得函数的最大值.点评:本题主要考查两个向量平行的性质,两个向量的数量积公式,两角和差的正弦公式,同角三角函数的基本关系,正弦函数的定义域和值域,属于中档题.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
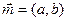 ,
,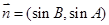 ,
,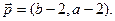
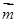 //
//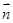 ,求证:ΔABC为等腰三角形;
,求证:ΔABC为等腰三角形; 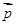 ,边长c = 2,角C =
,边长c = 2,角C = 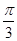 ,求ΔABC的面积 .
,求ΔABC的面积 . 的角
的角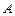 、
、 、
、 所对的边分别是
所对的边分别是 、
、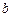 、
、 ,设向量
,设向量 ,
,
 ,
, .
. ,求证:
,求证: ,边长
,边长 ,角
,角 ,求
,求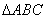
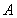
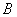
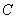

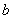
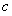
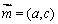
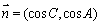
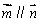
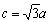
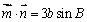
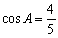
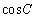
 ,
, ,
,
 ,求证△ABC为等腰三角形;
,求证△ABC为等腰三角形; ,边长
,边长 ,角
,角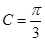 ,求△ABC的面积.
,求△ABC的面积.