题目内容
13、某校有6间不同的电脑室,每天晚上至少开放2间,欲求不同安排方案的种数,现有四位同学分别给出下列四个结果:
①C63+2C64+C65+C66;②C62;③26-7;④A62.其中所有正确的结果的序号是
①C63+2C64+C65+C66;②C62;③26-7;④A62.其中所有正确的结果的序号是
①③
.分析:对于②是只开放2间的方案数,故错误.对于①从正面分4种可能性求得至少开放2间的方案数,故正确.对于③求它的对立事件,不开放和开放1间的方案数,然后用总共的方案数减去对立面即可,故正确.对于④在此题中无意义故错误
解答:解:对于②显然错误,因为它求的是6间不相同的电脑室只开放2间的方案数.
对于①是电脑室开放2间的方案加上开放3间,4间,5间,6间的方案和.故正确.
对于③因为不开放和开放1间的方案7种,是至少开放2间的反面,故用总共的方案个数减去7亦所求,故正确.
对于④是排列问题在此题中无意义,显然错误.
即①和③正确.
故答案为:①③.
对于①是电脑室开放2间的方案加上开放3间,4间,5间,6间的方案和.故正确.
对于③因为不开放和开放1间的方案7种,是至少开放2间的反面,故用总共的方案个数减去7亦所求,故正确.
对于④是排列问题在此题中无意义,显然错误.
即①和③正确.
故答案为:①③.
点评:此题主要考查排列组合的简单计数问题和实际应用,题中需要对各种求法做分析判断,有一定的灵活性属于中档题目.

练习册系列答案
 名校名师培优作业本加核心试卷系列答案
名校名师培优作业本加核心试卷系列答案 全程金卷系列答案
全程金卷系列答案
相关题目
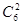 ②
②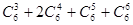 ③
③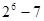 ④
④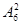 其中正确的结论是___
其中正确的结论是___