��Ŀ����
17����Դ�����³ǽ�һ���ţ����˵��Ŷ��ѽ��ã����������m�ף����¹���ֻ�轨�����Ŷ�֮���������Ŷգ���Ԥ�⣬һ���ŶյĹ��̷���Ϊ32��Ԫ������Ϊx����������֮������湤�̷���Ϊ��2+$\sqrt{x}$��x��Ԫ�������ŶյȾ���ֲ��������Ŷն���Ϊ�㣬�Ҳ������������أ������¹��̵ķ���Ϊy��Ԫ����1����д��y����x�ĺ�����ϵʽ��
��2����m=96��ʱ�����½����ٸ��Ŷղ���ʹ���¹��̵ķ���y��С��
���� ��1��������������Ŷպ����湤������Ȼ��������⽨�������ܷ����빤�����ĺ�����ϵ��
��2����m=96��ʱ��������֪��������ʽ�������ʱ�ĺ�������ʽ���������ݵ����뺯�������ԵĹ�ϵ�����ֵ�Լ���ʱx��ֵ��
��� �⣺��1�������½�n���Ŷգ���n+1��x=m����n=$\frac{m}{x}$-1������2�֣�
����y=f��x��=32n+��n+1����2+$\sqrt{x}$��x=32��$\frac{m}{x}$-1��+��2+$\sqrt{x}$��m
=m��$\frac{32}{x}$+$\sqrt{x}$��+2m-32���� 0��x��m������6�֣�
��2����m=96ʱ��f��x��=96��$\frac{32}{x}$+$\sqrt{x}$��+160
��f�䣨x��=$96��\frac{1}{{2\sqrt{x}}}-\frac{32}{x^2}��=\frac{48}{x^2}��{x^{\frac{3}{2}}}-64��$������8�֣�
��f�䣨x��=0����${x^{\frac{3}{2}}}$=64������x=16
��0��x��16ʱ��f�䣨x����0��f��x�������䣨0��16����Ϊ��������
��16��x��96��f�䣨x����0��f��x�������䣨16��96����Ϊ��������
����f��x����x=16��ȡ����Сֵ����ʱn=$\frac{96}{16}$-1=5����10�֣�
�����½�5���Ŷղ���ʹ���¹��̵ķ���y��С������12�֣�
���� ���⿼�麯��ģ�͵�ѡ����Ӧ�ã�ͨ����ʵ������ķ�����������ѧģ�ʹӶ�������⣮������Ҫ����һ�������ܷ����빤�����ĺ�����ϵ����ע��ȡֵ��Χ����Ҫ��֪ʶ���������ղ�Ӧ�ã������е��⣮

 �ƸԺ���ȫ�����Ų��Ծ�ϵ�д�
�ƸԺ���ȫ�����Ų��Ծ�ϵ�д�| A�� | ∅ | B�� | {1} | C�� | {x|-2��x��2} | D�� | {x|1��x��2} |
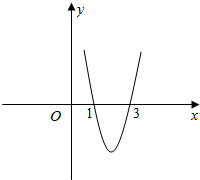 ��֪�溯��f��x���ڣ�0��+�ޣ��ϵ�ͼ����ͼ��ʾ����ʽ$\frac{f��x��}{x-1}��0$�Ľ⼯Ϊ��������
��֪�溯��f��x���ڣ�0��+�ޣ��ϵ�ͼ����ͼ��ʾ����ʽ$\frac{f��x��}{x-1}��0$�Ľ⼯Ϊ��������| A�� | ��-3��-1���ȣ�0��1���ȣ�1��3�� | B�� | ��-3��-1���ȣ�0��1���ȣ�3��+�ޣ� | C�� | ��-�ޣ�-3���ȣ�-1��0���ȣ�3��+�ޣ� | D�� | ��-�ޣ�-3���ȣ�-1��0���ȣ�0��1�� |
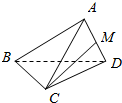 ��ͼ������A-BCD�У�AB=AC=BD=CD=3��AD=BC=2����M��AD���е㣬������ֱ��CM��AB���ɵĽ���$\frac{��}{4}$��
��ͼ������A-BCD�У�AB=AC=BD=CD=3��AD=BC=2����M��AD���е㣬������ֱ��CM��AB���ɵĽ���$\frac{��}{4}$��