Question

【题目】下列命题：①使得成立；②，都有成立，是在区间D上单调递增的充要条件；③只要函数有零点，我们就可以用二分法求出零点的近似值；④过点作直线，使它与抛物线仅有一个公共点，这样的直线有2条；正确的个数是（ ）

A.B.C.D.

Answer 1

【答案】D

【解析】

对于①，配方法说明恒成立，则①错误；对于②，举反例，即可说明②错误；对于③，举反例，说明③错误；对于④，求出满足题意的直线，共有3条，说明④错误，从而得解.

对于①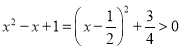，对恒成立，故①错误.

对于②，函数在上单调递增，其导数，，此时不满足“对，都有成立”，故②错误.

对于③，函数有一个零点，由于恒成立，不存在区间使得，故无法使用二分法求出零点的近似值，故③错误.

对于④，当斜率不存在时，直线方程为：，与抛物线仅有一个公共点，

当斜率存在时，设直线方程为，

当时，直线方程为：，与抛物线只有一个公共点，

当时，联立直线与抛物线方程，得，

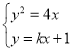消元整理得，

由题可知该方程有两个相等实根，

即，解得，

直线与抛物线只有一个公共点，

综上所述，与抛物线仅有一个公共点的直线有3条，故④错误.

正确的个数是.

故选：D.