题目内容
下列命题:
(1)方程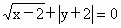 的解集为{2,-2}
的解集为{2,-2}
(2)集合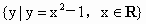 与
与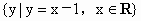 的公共元素所组成的集合是{0,1};
的公共元素所组成的集合是{0,1};
(3)集合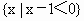 与集合
与集合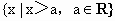 没有公共元素.
没有公共元素.
其中真命题的个数是
[ ]
|
A.0 |
B.1 |
C.2 |
D.3 |
答案:A
解析:
解析:
|
要判断这些命题的真假,这就需要对用来描述的这些命题的集合语言进行转化,以弄清集合的构成.在 (1)中方程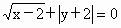 等价于 等价于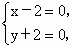 即 即 其解应为有序实数对,因此其解集应为{(2,-2)}故命题(1)是假命题,而在(2)中,由于集合 其解应为有序实数对,因此其解集应为{(2,-2)}故命题(1)是假命题,而在(2)中,由于集合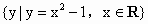 的代表元素是y,而y满足属性;“ 的代表元素是y,而y满足属性;“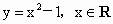 ”.由于当 ”.由于当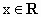 时, 时,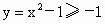 ,所以集合 ,所以集合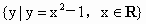 是由于大于或等于-1的实数所组成的集合.同理 是由于大于或等于-1的实数所组成的集合.同理 是R,因此(2)也是错误的.在(3)中,集合 是R,因此(2)也是错误的.在(3)中,集合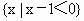 即为不等式x-1<0,即x<1的解集,而 即为不等式x-1<0,即x<1的解集,而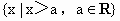 即为不等式x>a的解集,由图可知,这两个集合可能有公共的元素,也可能没有公共的元素,因此(3)也是错误的.故选A. 即为不等式x>a的解集,由图可知,这两个集合可能有公共的元素,也可能没有公共的元素,因此(3)也是错误的.故选A.
在 (2)中,很容易被符号描述法的表象所蒙蔽,认为这两个集合中的“x”和“y”必须取相同的值.事实上,这是用相同的字母来描述不同的集合的元素所具有的属性. |

练习册系列答案
相关题目
