题目内容
已知非零向量a,b,且a⊥b,求证: ≤
≤ .
.
 ≤
≤ .
.见解析
证明:a⊥b?a·b=0,要证 ≤
≤ .
.
只需证|a|+|b|≤ |a+b|,
|a+b|,
只需证|a|2+2|a||b|+|b|2≤2(a2+2a·b+b2),
只需证|a|2+2|a||b|+|b|2≤2a2+2b2,
只需证|a|2+|b|2-2|a||b|≥0,
即(|a|-|b|)2≥0,上式显然成立,故原不等式得证.
 ≤
≤ .
.只需证|a|+|b|≤
 |a+b|,
|a+b|,只需证|a|2+2|a||b|+|b|2≤2(a2+2a·b+b2),
只需证|a|2+2|a||b|+|b|2≤2a2+2b2,
只需证|a|2+|b|2-2|a||b|≥0,
即(|a|-|b|)2≥0,上式显然成立,故原不等式得证.

练习册系列答案
相关题目
 为三角形
为三角形 的三边,求证:
的三边,求证:
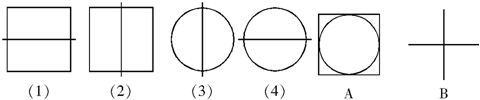
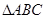 中,
中,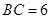 ,以
,以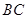 为直径的半圆分别交
为直径的半圆分别交 于点
于点 ,若
,若 ,则
,则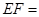


 _______
_______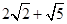 .
.