题目内容
已知锐角△ABC中,sin(A+B)=(1)求证:tanA=2tanB;
(2)设AB=3,求AB边上的高.
剖析:有两角的和与差联想到两角和与差的正弦公式,结合图形,以(1)为铺垫,解决(2).
(1)证明:∵sin(A+B)=![]() ,sin(A-B)=
,sin(A-B)=![]() ,
,
∴ =2.
=2.
∴tanA=2tanB.
(2)解:![]() <A+B<π,∴sin(A+B)=
<A+B<π,∴sin(A+B)=![]() .
.
∴tan(A+B)=-![]() ,
,
即![]() =-
=-![]() .将tanA=2tanB代入上式整理得2tan2B-4tanB-1=0,解得tanB=
.将tanA=2tanB代入上式整理得2tan2B-4tanB-1=0,解得tanB=![]() (负值舍去).得tanB=
(负值舍去).得tanB=![]() ,∴tanA=2tanB=2+
,∴tanA=2tanB=2+![]() .
.
设AB边上的高为CD,则AB=AD+DB=![]() +
+![]() =
=![]() .
.
由AB=3得CD=2+![]() ,∴AB边上的高为2+
,∴AB边上的高为2+![]() .
.
讲评:本题主要考查三角函数概念,两角和与差的公式以及应用,分析和计算能力.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
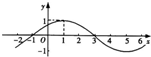 已知函数f(x)=Asin(ωx+φ)(其中x∈R,A?>0,ω>0,
已知函数f(x)=Asin(ωx+φ)(其中x∈R,A?>0,ω>0,