题目内容
设m,n∈N,f(x)=(1+2x)m+(1+x)n.
(1)当m=n=2014时,若f(x)的展开式可表示为f(x)=a0+a1x+a2x2+…+a2014x2014,求a0-a1+a2-…-a2014;
(2)若f(x)展开式中x的系数是20,则当m,n取何值时,x2系数最小,最小为多少?
(1)当m=n=2014时,若f(x)的展开式可表示为f(x)=a0+a1x+a2x2+…+a2014x2014,求a0-a1+a2-…-a2014;
(2)若f(x)展开式中x的系数是20,则当m,n取何值时,x2系数最小,最小为多少?
考点:二项式系数的性质
专题:二项式定理
分析:(1)当m=n=2014时,f(x)=(1+2x)2014+(1+x)2014 =a0+a1x+a2x2+…+a2014x2014,令x=-1可得 a0-a1+a2-…-a2014的值.
(2)因为f(x)展开式中x的系数是2
+
=20,即n=20-2m,则x2的系数为4m2-41m+190,再利用二次函数的性质求得它的最小值.
(2)因为f(x)展开式中x的系数是2
| C | 1 m |
| C | 1 n |
解答:
解:(1)当m=n=2014时,f(x)=(1+2x)2014+(1+x)2014 =a0+a1x+a2x2+…+a2014x2014,
令x=-1可得 a0-a1+a2-…-a2014=1.
(2)因为f(x)展开式中x的系数是2
+
=2m+n=20,
所以,n=20-2m,则x2的系数为 22•
+
=4×
+
=4m2-41m+190,
所以当m=5,即n=10时,展开式中的x2系数最小,最小值为85.
令x=-1可得 a0-a1+a2-…-a2014=1.
(2)因为f(x)展开式中x的系数是2
| C | 1 m |
| C | 1 n |
所以,n=20-2m,则x2的系数为 22•
| C | 2 m |
| C | 2 n |
| m(m-1) |
| 2 |
| n(n-1) |
| 2 |
所以当m=5,即n=10时,展开式中的x2系数最小,最小值为85.
点评:本题主要考查二项式定理的应用,注意根据题意,分析所给代数式的特点,通过给二项式的x赋值,求展开式的系数和,可以简便的求出答案,属于基础题.

练习册系列答案
相关题目
设向量
=(2,t)与向量
=(1,3)共线,则t等于( )
| a |
| b |
| A、-6 | ||
B、
| ||
C、
| ||
| D、6 |
已知等差数列{an}中,a2=2,a4=6,则前4项的和S4等于( )
| A、8 | B、10 | C、12 | D、14 |
设集合A={1,2,3,4,5},集合B={1,3,5},则集合A∩B=( )
| A、{2,4} |
| B、{1,2,3} |
| C、{1,3,5} |
| D、{1,2,3,4,5} |
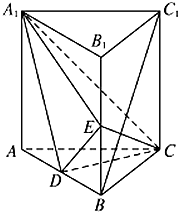 如图,直棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=
如图,直棱柱ABC-A1B1C1中,D,E分别是AB,BB1的中点,AA1=AC=CB=