题目内容
若一个等差数列的第1,2,3项分别为 ,那么这个数列的第101项为________.
,那么这个数列的第101项为________.

分析:根据等差中项得
 ,求出x的值,再求出此数列的前3项,进而求出d和an,再求出a101的值.
,求出x的值,再求出此数列的前3项,进而求出d和an,再求出a101的值.解答:由题意知,
 ,即
,即 ,
,∴
 ,解得,x=2,
,解得,x=2,∴这个等差数列的前3项分别为:
 ,
, ,
, ,∴公差d=
,∴公差d= ,
,∴通项公式an=
 +(n-1)×
+(n-1)× =
= +
+ ,
,∴a101=

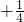 =
= ,
,故答案为:
 .
.点评:本题考查了等差数列的性质应用,即等差中项和通项公式的简单应用.

练习册系列答案
相关题目
 ,那么这个数列的第101项为 .
,那么这个数列的第101项为 .