题目内容
选修4-5:不等式选讲(本小题满分10分)
解不等式![]() .
.
(方法一)当![]() 时,∵原不等式即为
时,∵原不等式即为![]() ,这显然不可能,∴
,这显然不可能,∴![]() 不适合.
不适合.
当![]() 时,∵原不等式即为
时,∵原不等式即为![]() ,又
,又![]() ,∴
,∴![]() 适合.
适合.
当![]() 时,∵原不等式即为
时,∵原不等式即为![]() ,这显然恒成立,∴
,这显然恒成立,∴![]() 适合.
适合.
故综上知,不等式的解集为![]() ,即
,即![]()
(方法二)设函数![]() ,则∵
,则∵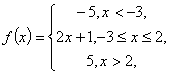 ∴作函数
∴作函数![]()
的图象,如图所示,并作直线![]() 与之交于点
与之交于点![]() .
.
又令![]() ,则
,则![]() ,即点
,即点![]() 的横坐标为
的横坐标为![]() .
.
故结合图形知,不等式的解集为![]() .
.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
题目内容
选修4-5:不等式选讲(本小题满分10分)
解不等式![]() .
.
(方法一)当![]() 时,∵原不等式即为
时,∵原不等式即为![]() ,这显然不可能,∴
,这显然不可能,∴![]() 不适合.
不适合.
当![]() 时,∵原不等式即为
时,∵原不等式即为![]() ,又
,又![]() ,∴
,∴![]() 适合.
适合.
当![]() 时,∵原不等式即为
时,∵原不等式即为![]() ,这显然恒成立,∴
,这显然恒成立,∴![]() 适合.
适合.
故综上知,不等式的解集为![]() ,即
,即![]()
(方法二)设函数![]() ,则∵
,则∵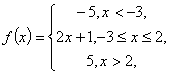 ∴作函数
∴作函数![]()
的图象,如图所示,并作直线![]() 与之交于点
与之交于点![]() .
.
又令![]() ,则
,则![]() ,即点
,即点![]() 的横坐标为
的横坐标为![]() .
.
故结合图形知,不等式的解集为![]() .
.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案