题目内容
在锐角△ABC中,若C=2B,则 的范围
的范围
- A.

- B.
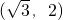
- C.(0,2)
- D.
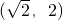
A
分析:由正弦定理得 ,再根据△ABC是锐角三角形,求出B,cosB的取值范围即可.
,再根据△ABC是锐角三角形,求出B,cosB的取值范围即可.
解答:由正弦定理得 ,∵△ABC是锐角三角形,∴三个内角均为锐角,
,∵△ABC是锐角三角形,∴三个内角均为锐角,
即有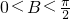
 ,0<π-C-B=π-3B<
,0<π-C-B=π-3B<
解得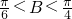 ,又余弦函数在此范围内是减函数.故
,又余弦函数在此范围内是减函数.故 <cosB<
<cosB< .
.
∴ <
< <
<
故选A
点评:本题考查了二倍角公式、正弦定理的应用、三角函数的性质.易错点是B角的范围确定不准确.
分析:由正弦定理得
 ,再根据△ABC是锐角三角形,求出B,cosB的取值范围即可.
,再根据△ABC是锐角三角形,求出B,cosB的取值范围即可.解答:由正弦定理得
 ,∵△ABC是锐角三角形,∴三个内角均为锐角,
,∵△ABC是锐角三角形,∴三个内角均为锐角,即有
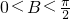
 ,0<π-C-B=π-3B<
,0<π-C-B=π-3B<
解得
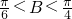 ,又余弦函数在此范围内是减函数.故
,又余弦函数在此范围内是减函数.故 <cosB<
<cosB< .
.∴
 <
< <
<
故选A
点评:本题考查了二倍角公式、正弦定理的应用、三角函数的性质.易错点是B角的范围确定不准确.

练习册系列答案
相关题目
在锐角△ABC中,若lg (1+sinA)=m,且lg
=n,则lgcosA等于( )
| 1 |
| 1-sinA |
A、
| ||||
| B、m-n | ||||
C、
| ||||
D、m+
|
已知函数f(x)=2sinxcosx+2
cos2x-
,x∈R
(I)化简函数f(x)的解析式,并求函数f(x)的最小正周期;
(Ⅱ)在锐角△ABC中,若f(A)=1,
•
=
,求△ABC的面积.
| 3 |
| 3 |
(I)化简函数f(x)的解析式,并求函数f(x)的最小正周期;
(Ⅱ)在锐角△ABC中,若f(A)=1,
| AB |
| AC |
| 2 |
在锐角△ABC中,若C=2B,则
的范围( )
| c |
| b |
A、(
| ||||
B、(
| ||||
| C、(0,2) | ||||
D、(
|