题目内容
已知,下图是计算函数f(x)在x处函数值的程序框图,其中a,a1,a2,a3,a4,a5,x是常数,且a5≠0,那么,这个函数是( )
A.f(x)=a5x+a4x+a3x+a2x+a1x+a
B.f(x)=a1x+a2x+a3x+a4x+a5
C.f(x)=a5x5+a4x4+a3x3+a2x2+a1x+a0
D.f(x)=a5x4+a4x3+a3x2+a2x+a1
【答案】分析:根据程序框图,本算法是利用秦九韶算法计算多项式的值,先将多项式转化为x(x(x(x(4x+2)+3)+4)-6)+5的形式,然后逐步计算v至v5的值,即可得到答案.
解答:解:观察程序图得:
求多项式的值时,首先计算最内层括号内一次多项式的值,即
v[1]=a[n]x+a[n-1]
然后由内向外逐层计算一次多项式的值,即
v[2]=v[1]x+a[n-2]
v[3]=v[2]x+a[n-3]
…
v[n]=v[n-1]x+a[0]
这样,f(x)=(…(anx+an-1)x+an-2)x+…+a1)x+a,
即这个函数是:f(x)=a5x5+a4x4+a3x3+a2x2+a1x+a0,
故选C.
点评:本题考查的知识点是程序框图、秦九韶算法,其中将多项式转化为x(x(x(x(4x+2)+3)-2)-2500)+434的形式,是解答本题的关键.
解答:解:观察程序图得:
求多项式的值时,首先计算最内层括号内一次多项式的值,即
v[1]=a[n]x+a[n-1]
然后由内向外逐层计算一次多项式的值,即
v[2]=v[1]x+a[n-2]
v[3]=v[2]x+a[n-3]
…
v[n]=v[n-1]x+a[0]
这样,f(x)=(…(anx+an-1)x+an-2)x+…+a1)x+a,
即这个函数是:f(x)=a5x5+a4x4+a3x3+a2x2+a1x+a0,
故选C.
点评:本题考查的知识点是程序框图、秦九韶算法,其中将多项式转化为x(x(x(x(4x+2)+3)-2)-2500)+434的形式,是解答本题的关键.

练习册系列答案
相关题目
 7、已知,下图是计算函数f(x)在x0处函数值的程序框图,其中a0,a1,a2,a3,a4,a5,x0是常数,且a5≠0,那么,这个函数是( )
7、已知,下图是计算函数f(x)在x0处函数值的程序框图,其中a0,a1,a2,a3,a4,a5,x0是常数,且a5≠0,那么,这个函数是( )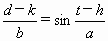 .
.
 已知,下图是计算函数f(x)在x0处函数值的程序框图,其中a0,a1,a2,a3,a4,a5,x0是常数,且a5≠0,那么,这个函数是
已知,下图是计算函数f(x)在x0处函数值的程序框图,其中a0,a1,a2,a3,a4,a5,x0是常数,且a5≠0,那么,这个函数是 ,下图是计算函数值y的流程图,则空白框中应该填上( )。
,下图是计算函数值y的流程图,则空白框中应该填上( )。