题目内容
15．
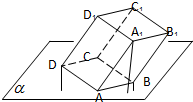多面体上，位于同一条棱两端的顶点称为相邻的，如图，正方体的一个顶点A在平面α内，其余顶点在α的同侧，正方体上与顶点A相邻的三个顶点到α的距离分别为1，2和4，P是正方体的其余四个顶点中的一个，则P到平面α的距离可能是：（2）（4）（5）（6）．（写出所有正确结论的编号）（1）2； （2）3； （3）4；（4）5； （5）6； （6）7．
分析 先求出线段BD的中点到平面α的距离，从而能求出C点到平面α的距离；B点到平面α的距离=A1点到平面α的距离+B点平面α；点C1到平面α的距离=点A1到平面α的距离+点C到平面α的距离；点D1到平面α的距离=点A1到平面α的距离+点D到平面α的距离．
解答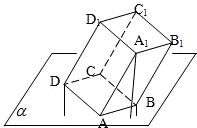 
解：如图，B、D、A1到平面α的距离分别为1、2、4，
则D、A1的中点到平面α的距离为3，
即A、D1的中点到平面α的距离为3
所以D1到平面α的距离为6；
同样地，B、A1的中点到平面α的距离为$\frac{5}{2}$，
所以B1到平面α的距离为5；
则D、B的中点到平面α的距离为$\frac{3}{2}$，
所以C到平面α的距离为3；
C、A1的中点到平面α的距离为$\frac{1}{2}$，
所以C1到平面α的距离为7；
∵P为C、C1、B1、D1中的一点，
∴P到平面α的距离可能是3，5，6，7．
故答案为：（2）（4）（5）（6）．
点评 本题考查点到平面的距离的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
阅读快车系列答案
相关题目
将边长为2的正方形ABCD沿对角线BD折叠，使得平面ABD⊥平面CBD，AE⊥平面ABD，且AE=$\frac{PC}{PA}=\frac{CA}{AB}$．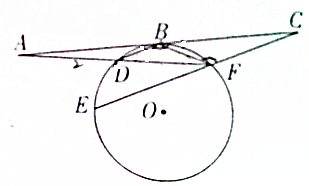
已知直线AC与⊙O相切于点B，AD交⊙O于F、D两点，CF交⊙O于E、F，BD∥CE，AB=BC，AD=2，BD=1
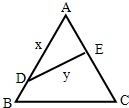如图，某公园有一块边长为2的等边△ABC的边角地，现修成草坪，图中DE把草坪分成面积相等的两部分，D在AB上，E在AC上．
7．若偶函数f（x）在（-∞，-1]上是减函数，则（ ）
| A． | $f（π）＜f（-\frac{3}{2}）＜f（1）$ | B． | $f（π）＜f（1）＜f（-\frac{3}{2}）$ | C． | $f（-\frac{3}{2}）＜f（1）＜f（π）$ | D． | $f（1）＜f（-\frac{3}{2}）＜f（π）$ |