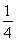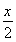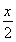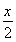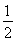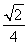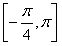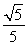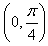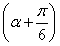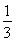题目内容

函数f(x)＝sinsin＋sinxcosx(x∈R)．

(1)求f的值；

(2)在△ABC中，若f＝1，求sinB＋sinC的最大值．

 

（1）1（2）

【解析】(1)f(x)＝sinsin＋sinxcosx＝

cos2x＋sin2x＝sin，所以f＝1.

(2)因为f＝1，所以sin＝1.

因为0＜A＜π，所以A＋＝，即A＝.

sinB＋sinC＝sinB＋sin＝sinB＋cosB＝sin.

因为0＜B＜，所以＜B＋＜，所以＜sin≤1，

所以sinB＋sinC的最大值为.

 

练习册系列答案
相关题目

在△ABC中，a＝3，b＝2，∠B＝2∠A.

(1)求cosA的值；

(2)求c的值．

 

在△ABC中，∠A、∠B、∠C所对的边分别为a、b、c，若a＝1，b＝2，cosC＝.求：

(1)△ABC的周长；

(2)cos(A－C)的值．

 

已知△ABC的三边长分别为a、b、c，且a2＋b2－c2＝ab，则∠C＝________．

 

已知函数f(x)＝sincos＋cos2－

(1)若f(α)＝，α∈(0，π)，求α的值；

(2)求函数f(x)在上最大值和最小值．

 

已知sin2α＝，且α∈，则sin4α－cos4α＝________．

 

已知sin＝，则cos＝________．

 

已知α为第二象限角，sinα＋cosα＝，则cos2α＝________．

 

如图，它表示电流I＝Asin(ωt＋φ)(A>0，ω>0)在一个周期内的图象，则I＝Asin(ωt＋φ)的解析式为________________．

 

 

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网