题目内容
数列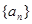 的前
的前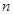 项和为
项和为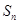 ,且
,且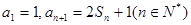 ,数列
,数列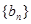 为等差数列,且
为等差数列,且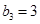 ,
, .
.
(1)求数列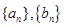 的通项公式;
的通项公式;
(2)若对任意的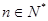 ,
,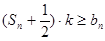 恒成立,求实数
恒成立,求实数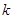 的取值范围.
的取值范围.
(1)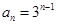 ,
,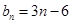 ;(2)
;(2)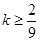 .
.
解析试题分析:本题主要考查等差数列的通项公式、等比数列的通项公式和前n项和公式、恒成立问题等基础知识,考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问,因为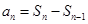 ,利用①②2个式子作差,得到
,利用①②2个式子作差,得到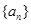 为等比数列,利用等比数列的通项公式直接写出
为等比数列,利用等比数列的通项公式直接写出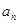 代入已知中,得到
代入已知中,得到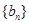 为等差数列;第二问,利用等比数列的前n项和公式先计算出
为等差数列;第二问,利用等比数列的前n项和公式先计算出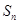 ,先将恒成立问题转化为
,先将恒成立问题转化为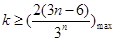 ,利用
,利用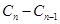 的正负判断数列
的正负判断数列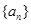 的单调性,求出数列的最大值,从而得到k的取值范围.
的单调性,求出数列的最大值,从而得到k的取值范围.
试题解析:(1)因为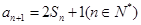 …①
…①
所以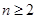 时,
时,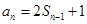 …②
…②
①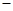 ②得
②得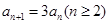
又因为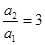 ,所以
,所以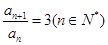 ,所以
,所以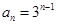
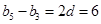 ,所以
,所以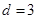 ,所以
,所以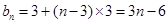
(2)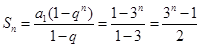
所以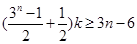 对
对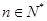 恒成立,即
恒成立,即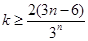 对
对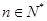 恒成立
恒成立
令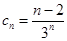 ,
,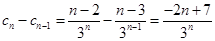
当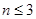 时,
时,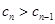 ;当
;当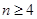 时,
时,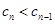 ,所以
,所以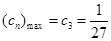
所以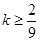
考点:等差数列的通项公式、等比数列的通项公式和前n项和公式、恒成立问题.

练习册系列答案
相关题目
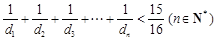 .
.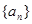 的前
的前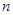 项和为
项和为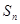 ,
,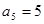 ,
,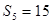 ,
,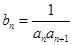 ,求数列
,求数列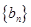 的前100项和.
的前100项和.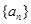 中,已知
中,已知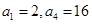 .
.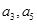 分别为等差数列
分别为等差数列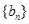 的第3项和第5项,试求数列
的第3项和第5项,试求数列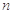 项和
项和 .
.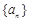 满足
满足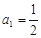 ,
,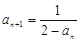
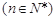 .
.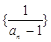 为等差数列,并求出
为等差数列,并求出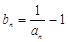 ,数列
,数列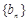 的前
的前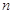 项和为
项和为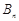 ,对任意
,对任意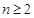 都有
都有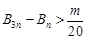 成立,求整数
成立,求整数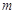 的最大值.
的最大值. 中,
中,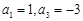 .
.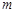 项和
项和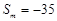 ,求
,求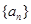 的各项均为正数,记
的各项均为正数,记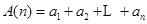 ,
,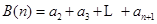 ,
,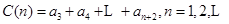 .
.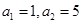 ,且对任意
,且对任意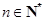 ,三个数
,三个数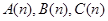 组成等差数列,求数列
组成等差数列,求数列 的等比数列的充分必要条件是:对任意
的等比数列的充分必要条件是:对任意