题目内容
数列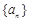 满足
满足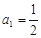 ,
,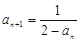
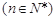 .
.
(1)求证: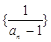 为等差数列,并求出
为等差数列,并求出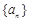 的通项公式;
的通项公式;
(2)设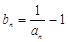 ,数列
,数列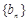 的前
的前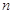 项和为
项和为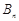 ,对任意
,对任意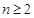 都有
都有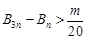 成立,求整数
成立,求整数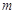 的最大值.
的最大值.
(1) (2)18
(2)18
解析试题分析:(1)要证明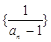 是等差数列,只需证明
是等差数列,只需证明 是常数,所以根据题意,利用
是常数,所以根据题意,利用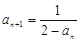 ,化简
,化简 ,即可证明.
,即可证明.
(2)将(1)中结论代入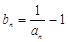 ,而后设出
,而后设出 ,根据题意只需找到
,根据题意只需找到 的最小值,令最小值大于
的最小值,令最小值大于 .所以得判断数列
.所以得判断数列 的增减性,利用
的增减性,利用 ,放缩判断其与0的大小关系.而后根据
,放缩判断其与0的大小关系.而后根据 ,可得结论.
,可得结论.
试题解析:(1)



∴
∴ 为首次为-2,公差为-1的等差数列
为首次为-2,公差为-1的等差数列
∴

∴
(2) 令
令
∴ =
=
=
∴ ∴
∴ 为单调递增数列
为单调递增数列
∴ ∴
∴
∴ 又
又 所以
所以 的最大值为18
的最大值为18
考点:等差数列的证明;放缩法判断数列的增减性.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目
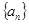 ( n∈N*)中a1>1,公比q>0,设bn=log2an,且b1+b3+b5=6,b1·b3·b5=0.
( n∈N*)中a1>1,公比q>0,设bn=log2an,且b1+b3+b5=6,b1·b3·b5=0.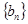 是等差数列;
是等差数列;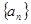 中,
中,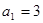 ,其前
,其前 项和为
项和为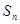 ,等比数列
,等比数列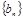 的各项均为正数,
的各项均为正数, ,公比为
,公比为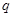 ,且
,且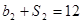 ,
,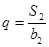 .
.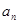 与
与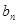 ; (2)设数列
; (2)设数列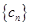 满足
满足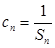 ,求
,求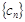 的前
的前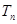 .
.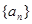 的前
的前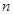 项和为
项和为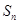 ,且
,且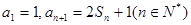 ,数列
,数列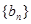 为等差数列,且
为等差数列,且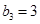 ,
, .
.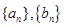 的通项公式;
的通项公式;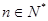 ,
,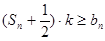 恒成立,求实数
恒成立,求实数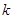 的取值范围.
的取值范围.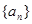 的前n项和为
的前n项和为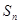 ,且
,且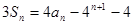
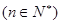 ,令
,令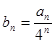 .
.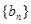 是等差数列,并求数列
是等差数列,并求数列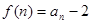
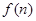 是18的倍数.
是18的倍数. 的前
的前 项和为
项和为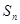 ,
, ,
,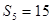 ,
, ,求数列
,求数列 的前100项和.
的前100项和.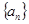 的前
的前 项和
项和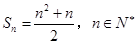 .
.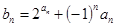 ,求数列
,求数列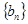 的前
的前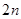 项和.
项和.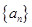 中,其前
中,其前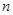 项和为
项和为 ,且
,且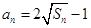 .
.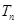 是数列
是数列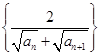 的前
的前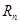 是数列
是数列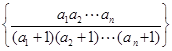 的前
的前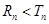 .
.