题目内容
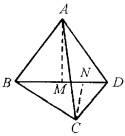
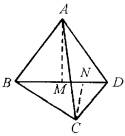
(1)如图所示，空间四边形ABCD中，AB=AD，BC≠DC，作AM⊥BD于M，CN⊥BD于N，证明：AM与CN异面．
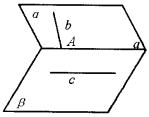
(2)如图所示，已知a ∩b =a，b
a ，c
b ，且b∩a=A，c∥a，求证：b和c为异面直线．
答案：
解析：
解析：
证明：(1)∵ AB=AD，∴ M为BD中点． 又∵ BC≠DC，∴ N不是BD中点，从而M，N两点不重合． (2)反证． 若b，c共面，则b∩c或b∥c． 若b∥c，∵ a∥c 若b∩c，则b，c确定平面g，又∵ A∈a∥c， ∴ A不在直线c上，从而面b、g同时过直线c及其外一点A，从而b与g重合． ∵ b |
a
练习册系列答案
阅读快车系列答案
相关题目
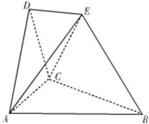在如图所示的空间几何体中，△ABC，△ACD都是等边三角形，AE=CE，DE∥平面ABC，平面ACD⊥平面ABC．
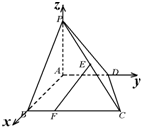已知ABCD为直角梯形，AD∥BC，∠BAD=90°，PA=AD=AB=1，BC=2，E为PC的中点，PA⊥平面ABCD，建立如图所示的空间直角坐标系．
已知正三棱柱ABC-A1B1C1，底面边长AB=2，AB1⊥BC1，点O、O1分别是边AC，A1C1的中点，建立如图所示的空间直角坐标系．
