题目内容
一袋子中有大小相同的2个红球和3个黑球,从袋子里随机取球取到每个球的可能性是相同的,设取到一个红球得2分,取到一个黑球得1分.
(1)若从袋子里一次随机取出3个球,求得4分的概率;
(2)若从袋子里每次摸出一个球,看清颜色后放回,连续摸2次,求得分ξ的概率分布列及数学期望.
(1)若从袋子里一次随机取出3个球,求得4分的概率;
(2)若从袋子里每次摸出一个球,看清颜色后放回,连续摸2次,求得分ξ的概率分布列及数学期望.
分析:设“ξ=所得分数”(1)由ξ=4表示取到的3个球中有2个黑球,1个红球,能求出P(ξ=4).
(2)由题设知ξ的可能取值为2,3,4.分别求出P(ξ=2),P(ξ=3),P(ξ=4),由此能求出ξ的分布列和Eξ.
(2)由题设知ξ的可能取值为2,3,4.分别求出P(ξ=2),P(ξ=3),P(ξ=4),由此能求出ξ的分布列和Eξ.
解答:解:设“ξ=所得分数”
(1)∵ξ=4表示取到的3个球中有2个黑球,1个红球,
∴P(ξ=4)=
=
.(4分)
(2)∵ξ=2表示取到的2个球都是黑球,
∴P(ξ=2)=(
)2=
,
∵ξ=3表示取到的2个球中有1个黑球,1个红球,
∴P(ξ=3)=
•
•
=
,
∵ξ=4表示取到的2个球都是红球,
∴P(ξ=4)=(
)2 =
,(10分)
分布列为:
(12分)
∴期望为:Eξ=2×
+3×
+4×
=
.(14分)
(1)∵ξ=4表示取到的3个球中有2个黑球,1个红球,
∴P(ξ=4)=
| ||||
|
| 3 |
| 5 |
(2)∵ξ=2表示取到的2个球都是黑球,
∴P(ξ=2)=(
| 3 |
| 5 |
| 9 |
| 25 |
∵ξ=3表示取到的2个球中有1个黑球,1个红球,
∴P(ξ=3)=
| C | 1 2 |
| 3 |
| 5 |
| 2 |
| 5 |
| 12 |
| 25 |
∵ξ=4表示取到的2个球都是红球,
∴P(ξ=4)=(
| 2 |
| 5 |
| 4 |
| 25 |
分布列为:
| ξ | 2 | 3 | 4 | ||||||
P |
|
|
|
∴期望为:Eξ=2×
| 9 |
| 25 |
| 12 |
| 25 |
| 4 |
| 25 |
| 14 |
| 5 |
点评:本题考查离散型随机变量的数学期望和方差,是中档题,是历年高考的必考题型之一.解题时要认真审题,仔细解答,注意合理地进行等价转化.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
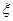 的概率分布列及数学期望。
的概率分布列及数学期望。 的概率分布列及数学期望。
的概率分布列及数学期望。