题目内容
8. 某几何体的三视图如图所示,则这个几何体的体积为( )
某几何体的三视图如图所示,则这个几何体的体积为( )| A. | $\frac{\sqrt{3}}{6}$π | B. | $\frac{\sqrt{3}}{2}π$ | C. | $\frac{2\sqrt{3}}{3}π$ | D. | $\frac{4\sqrt{3}}{3}π$ |
分析 由已知中的三视图,可得该几何体是一个半圆柱和一个半圆锥的组合体,分别计算半圆柱和半圆锥的体积,相加可得答案.
解答 解:由已知中的三视图,可得该几何体是一个半圆柱和一个半圆锥的组合体,
底面半径均为1,高均为$\sqrt{3}$,
故半圆柱的体积为:$\frac{1}{2}×π•{1}^{2}×\sqrt{3}$=$\frac{\sqrt{3}}{2}π$,
半圆锥的体积为:$\frac{1}{3}×\frac{1}{2}×π•{1}^{2}×\sqrt{3}$=$\frac{\sqrt{3}}{6}π$,
故组合体的体积V=$\frac{\sqrt{3}}{2}π$+$\frac{\sqrt{3}}{6}π$=$\frac{2\sqrt{3}}{3}π$,
故选:C.
点评 本题考查的知识点是由三视图求体积和表面积,根据三视图判断出几何体的形状是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
13.对于任意实数a,b,定义max{a,b}=$\left\{\begin{array}{l}{a,a≥b}\\{b,a<b}\end{array}\right.$,已知在[-2,2]上的偶函数f(x)满足当0≤x≤2时,f(x)=max{2x-1,2-x}若方程f(x)-mx+1=0恰有两个根,则m的取值范围是( )
| A. | [-2,-eln2)∪(eln2,2] | B. | [-eln2,0)∪(0,eln2] | C. | [-2,0)∪(0,2] | D. | [-e,-2)∪(2,e] |
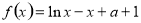 .
.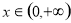 使得
使得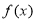 ≥0成立,求
≥0成立,求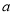 的范围;
的范围;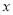 >1时,在(1)的条件下,
>1时,在(1)的条件下,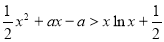 成立.
成立.