题目内容
【题目】已知函数![]() .
.
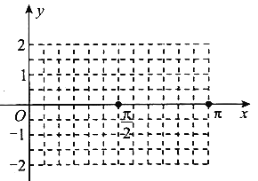
(1)若![]() ,用“五点法”在给定的坐标系中,画出函数
,用“五点法”在给定的坐标系中,画出函数![]() 在
在![]() 上的图象;
上的图象;
(2)若![]() 为奇函数,求
为奇函数,求![]() ;
;
(3)在(2)的前提下,将函数![]() 的图象向左平移
的图象向左平移![]() 个单位后,再将得到的图象上各点的横坐标伸长为原来的2倍,纵坐标不变,得到函数
个单位后,再将得到的图象上各点的横坐标伸长为原来的2倍,纵坐标不变,得到函数![]() 的图象,求
的图象,求![]() 在
在![]() 上的单调递增区间.
上的单调递增区间.
【答案】(1)图象见解析;(2)![]() ;(3)
;(3)![]()
【解析】
(1)利用“五点法”列表、描点即可得到函数的图象;
(2)利用奇函数![]() 可构造方程求得
可构造方程求得![]() 的可能取值,结合
的可能取值,结合![]() 的范围求得结果;
的范围求得结果;
(3)将函数变为![]() ,根据三角函数左右平移和伸缩变换原则可得到
,根据三角函数左右平移和伸缩变换原则可得到![]() ,令
,令![]() 可求得
可求得![]() 的单调递增区间,从中截取位于
的单调递增区间,从中截取位于![]() 之间的部分即可.
之间的部分即可.
(1)当![]() 时,
时,![]() ,列表:
,列表:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
则函数![]() 在区间
在区间![]() 上的图象是:
上的图象是:

(2)![]() 为奇函数
为奇函数![]()
![]() ,
,![]()
![]()
(3)由(2)知:![]()
将![]() 向左平移
向左平移![]() 个单位,再将横坐标变为原来的
个单位,再将横坐标变为原来的![]() 倍,得到:
倍,得到:![]()
令![]() ,
,![]() ,解得:
,解得:![]() ,
,![]()
![]() 的单调递增区间为
的单调递增区间为![]()
![]() 在
在![]() 上的单调递增区间为
上的单调递增区间为![]()

 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案 小题狂做系列答案
小题狂做系列答案【题目】某生产企业研发了一种新产品,该新产品在某网店试销一个阶段后得到销售单价![]() 和月销售量
和月销售量![]() 之间的一组数据,如下表所示:
之间的一组数据,如下表所示:
销售单价 | 9 | 9.5 | 10 | 10.5 | 11 |
月销售量 | 11 | 10 | 8 | 6 | 5 |
(Ⅰ)根据统计数据,求出![]() 关于
关于![]() 的回归直线方程,并预测月销售量不低于12万件时销售单价的最大值;
的回归直线方程,并预测月销售量不低于12万件时销售单价的最大值;
(Ⅱ)生产企业与网店约定:若该新产品的月销售量不低于10万件,则生产企业奖励网店1万元;若月销售量不低于8万件且不足10万件,则生产企业奖励网店5000元;若月销售量低于8万件,则没有奖励.现用样本估计总体,从上述5个销售单价中任选2个销售单价,求抽到的产品含有月销量量不低于10万件的概率.
参考公式:对于一组数据![]() ,
,![]() ,…,
,…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为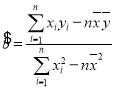 ,
,![]() .
.
参考数据:![]() ,
,![]() .
.
【题目】为了解某冷饮店的经营状况,随机记录了该店![]() 月的月营业额
月的月营业额![]() (单位:万元)与月份
(单位:万元)与月份![]() 的数据,如下表:
的数据,如下表:
|
|
|
|
|
|
|
|
|
|
|
|
(1)求![]() 关于
关于![]() 的回归直线方程
的回归直线方程![]() ;
;
(2)若在这样本点中任取两点,求恰有一点在回归直线上的概率.
附:回归直线方程![]() 中,
中,

 ,
,![]() .
.