题目内容
在△ABC中,已知sinA=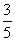 ,sinA+cosA<0,a=
,sinA+cosA<0,a=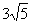 ,b=5,求c。
,b=5,求c。
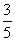 ,sinA+cosA<0,a=
,sinA+cosA<0,a=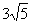 ,b=5,求c。
,b=5,求c。 解:因为sinA+cosA<0,且sinA=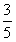 ,
,
所以cosA=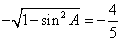 ,
,
又因为a=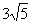 ,b=5,
,b=5,
所以由a2=b2+c2-2bccosA得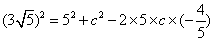 ,
,
即c2+8c-20=0,解得c=2或c=-10(舍去),
所以c=2。
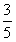 ,
,所以cosA=
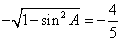 ,
,又因为a=
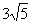 ,b=5,
,b=5,所以由a2=b2+c2-2bccosA得
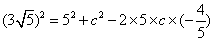 ,
,即c2+8c-20=0,解得c=2或c=-10(舍去),
所以c=2。

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
在△ABC中,已知|
|=4,|
|=1,S△ABC=
,则
•
的值为( )
| AB |
| AC |
| 3 |
| AB |
| AC |
| A、-2 | B、2 | C、±4 | D、±2 |