题目内容
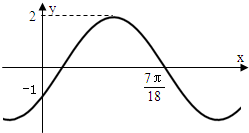 (2012•葫芦岛模拟)已知函数y=Asin(ωx+φ)(ω>0,|φ|<
(2012•葫芦岛模拟)已知函数y=Asin(ωx+φ)(ω>0,|φ|<| π |
| 2 |
| ω |
| φ |
分析:由函数的图象可得 A=2,再把点(0,-1)代入可得sinφ=-
. 再由|φ|<
可得 φ=-
.再把点(
,0)代入函数解析式可得2sin(ω•
-
)=0,求得ω=3,从而求得 则
的值.
| 1 |
| 2 |
| π |
| 2 |
| π |
| 6 |
| 7π |
| 18 |
| 7π |
| 18 |
| π |
| 6 |
| ω |
| φ |
解答:解:由函数的图象可得 A=2,再把点(0,-1)代入可得 2sin(0+φ)=-1,即sinφ=-
. 再由ω>0,|φ|<
可得 φ=-
.
由于图象过点(
,0)可得 2sin(ω•
-
)=0.ω•
-
=π,∴ω=3,
∴
=-
,
故选C.
| 1 |
| 2 |
| π |
| 2 |
| π |
| 6 |
由于图象过点(
| 7π |
| 18 |
| 7π |
| 18 |
| π |
| 6 |
| 7π |
| 18 |
| π |
| 6 |
∴
| ω |
| φ |
| 18 |
| π |
故选C.
点评:本题主要考查利用y=Asin(ωx+φ)的图象特征,由函数y=Asin(ωx+φ)的部分图象求解析式,属于中档题.

练习册系列答案
相关题目
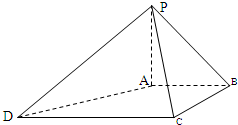 (2012•葫芦岛模拟)在四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,AB⊥BC,PA=AB=BC=
(2012•葫芦岛模拟)在四棱锥P-ABCD中,PA⊥底面ABCD,AB∥CD,AB⊥BC,PA=AB=BC=