题目内容
如图,在 中,
中, ,
, ,
, ,则
,则 等于( )
等于( )
A. | B. | C. | D. |

B
解析试题分析:



 .
.
考点:平面向量的性质、运算的几何意义.

练习册系列答案
相关题目
已知 和点
和点 满足
满足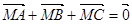 .若存在实数
.若存在实数 使得
使得 成立,则
成立,则 =( )
=( )
| A.2 | B.3 | C.4 | D.5 |
在 所在的平面内,点
所在的平面内,点 满足
满足 ,
, ,且对于任意实数
,且对于任意实数 ,恒有
,恒有
 ,则( )
,则( )
A. | B. | C.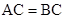 | D. |
如图,在 中,
中, ,延长
,延长 到
到 ,使
,使 ,若
,若 ,则
,则 的值是 ( )
的值是 ( )
A. | B. | C. | D. |
已知向量m,n满足m=(2,0),n= ,在
,在 中,若
中,若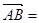 2m
2m 2n,
2n, 2m-6n,D是BC的中点,则|
2m-6n,D是BC的中点,则| |=
|=
| A.2 | B.4 | C.6 | D.8 |
设 是两个非零向量,下列选项正确的是( )
是两个非零向量,下列选项正确的是( )
A.若 ,则 ,则 |
B.若 ,则 ,则 |
C.若 ,则存在实数 ,则存在实数 ,使得 ,使得 |
D.若存在实数 ,使得 ,使得 ,则 ,则 |
以下说法错误的是( )
| A.零向量与任一非零向量平行 | B.零向量与单位向量的模不相等 |
| C.平行向量方向相同 | D.平行向量一定是共线向量 |
若 为
为 所在平面内一点,且满足
所在平面内一点,且满足 ,
,
则 的形状为( )
的形状为( )
| A.等腰三角形 | B.直角三角形 | C.正三角形 | D.等腰直角三角形 |
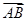 与
与 是两平行向量
是两平行向量 ,则A、B、C、D四点构成平行四边形
,则A、B、C、D四点构成平行四边形