题目内容
下列命题中的真命题是
- A.

- B.若
 ,则
,则 或
或
- C.
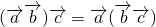
- D.若
 ,则
,则
D
分析:对于A:由于 ,故A不正确;对于B:若
,故A不正确;对于B:若 ,则
,则 与
与 垂直,不一定有:
垂直,不一定有: 或
或 ;由于 (
;由于 (  •
• )
)  表示一个与
表示一个与  平行的向量,而(
平行的向量,而(  •
• )
)  表示一个与
表示一个与  平行的向量,而
平行的向量,而  与
与  的大小方向都不确定,故C不一定成立.对于D:由于若
的大小方向都不确定,故C不一定成立.对于D:由于若 ,则
,则 ,从而得:则
,从而得:则 .
.
解答:对于A:由于 ,故A不正确;
,故A不正确;
对于B:若 ,则
,则 与
与 垂直,不一定有:
垂直,不一定有: 或
或 ,故B错;
,故B错;
由于 ( •
• )
)  表示一个与
表示一个与  平行的向量,而(
平行的向量,而(  •
• )
)  表示一个与
表示一个与  平行的向量,而
平行的向量,而  与
与  的大小方向都不确定,故C不一定成立.
的大小方向都不确定,故C不一定成立.
对于D:由于若 ,则
,则 ,从而得:则
,从而得:则 ,故D正确.
,故D正确.
故选D.
点评:本题考查两个向量的数量积公式的应用,两个向量的加减法的法则,以及其几何意义,正确利用两个向量运算的几何意义,是解题的难点.
分析:对于A:由于
 ,故A不正确;对于B:若
,故A不正确;对于B:若 ,则
,则 与
与 垂直,不一定有:
垂直,不一定有: 或
或 ;由于 (
;由于 (  •
• )
)  表示一个与
表示一个与  平行的向量,而(
平行的向量,而(  •
• )
)  表示一个与
表示一个与  平行的向量,而
平行的向量,而  与
与  的大小方向都不确定,故C不一定成立.对于D:由于若
的大小方向都不确定,故C不一定成立.对于D:由于若 ,则
,则 ,从而得:则
,从而得:则 .
.解答:对于A:由于
 ,故A不正确;
,故A不正确;对于B:若
 ,则
,则 与
与 垂直,不一定有:
垂直,不一定有: 或
或 ,故B错;
,故B错;由于 (
 •
• )
)  表示一个与
表示一个与  平行的向量,而(
平行的向量,而(  •
• )
)  表示一个与
表示一个与  平行的向量,而
平行的向量,而  与
与  的大小方向都不确定,故C不一定成立.
的大小方向都不确定,故C不一定成立.对于D:由于若
 ,则
,则 ,从而得:则
,从而得:则 ,故D正确.
,故D正确.故选D.
点评:本题考查两个向量的数量积公式的应用,两个向量的加减法的法则,以及其几何意义,正确利用两个向量运算的几何意义,是解题的难点.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目