题目内容
已知某个几何体的三视图如图，其中俯视图为正三角形，A1B1=2，A1A=4．根据图中标出的尺寸（单位cm ），可得这个几何体的表面积是24+2
cm2
| 3 |
24+2
cm2
．| 3 |
分析：先根据三视图确定这个几何体的形状，再根据几何体表面积计算公式计算即可
解答：解：这个几何体是一个正三棱柱，它的底面边长为2，高为4
∴此三棱柱的一个底面积为S△ABC=
×2×2×sin60°=
三棱柱的侧面积为S侧=（2+2+2）×4=24
∴这个几何体的表面积为S=S侧+2S△ABC=24+2
故答案为24+2
cm2
∴此三棱柱的一个底面积为S△ABC=
| 1 |
| 2 |
| 3 |
三棱柱的侧面积为S侧=（2+2+2）×4=24
∴这个几何体的表面积为S=S侧+2S△ABC=24+2
| 3 |
故答案为24+2
| 3 |
点评：本题考查了三视图的识图和空间图形的结构特征，柱体表面积计算公式，空间想象力
练习册系列答案
相关题目
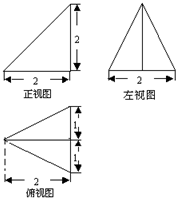已知某个几何体的三视图如图所示，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是
已知某个几何体的三视图如图，根据图中标出的尺寸（单位：cm），可得这个几何体的体积是（ ）
（1）已知某个几何体的三视图如图（主视图的弧线是半圆），根据图中的数据，求这个组合体的体积；
已知某个几何体的三视图如图，根据图中标出的尺寸（单位：cm），可得这个几何体的表面积是（ ）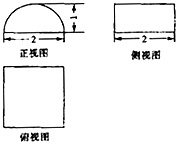
已知某个几何体的三视图如图（正视图中的弧线是半圆），图中标出的尺（单位：cm），可得这个几何体表面是