题目内容
设函数f(x)=x3-3ax2+3bx的图象与直线12x+y-1=0相切于点（1，-11），
（Ⅰ）求a，b的值；
（Ⅱ）讨论函数f（x）的单调性。
（Ⅰ）求a，b的值；
（Ⅱ）讨论函数f（x）的单调性。
解：（Ⅰ）求导得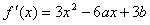
，
由于f（x）的图象与直线12x+y-1=0相切于点（1，-11），
所以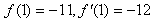
，
即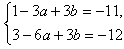
，解得a=1，b=-3。
（Ⅱ）由a=1，b=-3得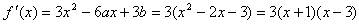
，
令f′（x）＞0，解得x＜-1或x＞3；又令f′（x）＜0，解得-1＜x＜3；
所以当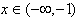
时，f（x）是增函数；当
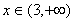时，f（x）也是增函数；
但x∈（-1，3）时，f（x）是减函数。
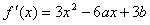，由于f（x）的图象与直线12x+y-1=0相切于点（1，-11），
所以
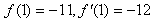，即
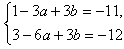，解得a=1，b=-3。（Ⅱ）由a=1，b=-3得
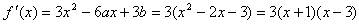，令f′（x）＞0，解得x＜-1或x＞3；又令f′（x）＜0，解得-1＜x＜3；
所以当
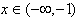时，f（x）是增函数；当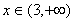时，f（x）也是增函数；但x∈（-1，3）时，f（x）是减函数。
练习册系列答案
相关题目
设函数f(x)=x3-(
)x-2，则其零点所在区间为（ ）
| 1 |
| 2 |
| A、（0，1） |
| B、（1，2） |
| C、（2，3） |
| D、（3，4） |