题目内容
过点(3,1)作圆(x-1)2+y2=1的两条切线,切点分别为A,B,则直线AB的方程为( )
| A.2x+y-3=0 | B.2x-y-3=0 | C.4x-y-3=0 | D.4x+y-3=0 |
A
解析试题分析:因为过点(3,1)作圆(x-1)2+y2=1的两条切线,切点分别为A,B,所以圆的一条切线方程为y=1,切点之一为(1,1),显然B、D选项不过(1,1),B、D不满足题意;另一个切点的坐标在(1,-1)的右侧,所以切线的斜率为负,选项C不满足,A满足.故选A.
考点:1.圆的切线方程;2.直线的一般式方程.

练习册系列答案
 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案
相关题目
过点P 和Q
和Q 的直线斜率为1,那么
的直线斜率为1,那么 的值为( )
的值为( )
| A.1 | B.4 | C.1或3 | D.1或4 |
已知点 ,
, ,
, ,若线段
,若线段 和
和 有相同的垂直平分线,则点
有相同的垂直平分线,则点 的坐标是( )
的坐标是( )
A. | B. |
C. | D. |
过两点A ,B(
,B( ,
, 的直线倾斜角是
的直线倾斜角是 ,则
,则 的值是( )
的值是( )
A. | B.3 | C.1 | D. |
过两点 的直线在
的直线在 轴上的截距为( ).
轴上的截距为( ).
A. | B. | C. | D. |
[2014·长春三校调研]一次函数y=- x+
x+ 的图象同时经过第一、三、四象限的必要不充分条件是( )
的图象同时经过第一、三、四象限的必要不充分条件是( )
| A.m>1,且n<1 | B.mn<0 |
| C.m>0,且n<0 | D.m<0,且n<0 |
点A(1,1)到直线xcosθ+ysinθ-2=0的距离的最大值是( )
| A.2 | B.2-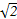 |
C.2+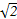 | D.4 |
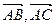 为一组邻边的平行四边形的面积S;
为一组邻边的平行四边形的面积S;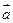 分别与向量
分别与向量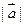 =
= ,求向量
,求向量