题目内容
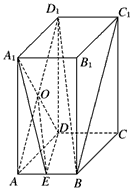
如图,长方体ABCD-A1B1C1D1中,AB=1,AA1=AD=2,点E为AB中点,
(1)求三棱锥A1-ADE的体积;
(2)求证:A1D⊥平面ABC1D1;
(3)求证:BD1∥平面A1DE。
(1)求三棱锥A1-ADE的体积;
(2)求证:A1D⊥平面ABC1D1;
(3)求证:BD1∥平面A1DE。
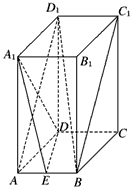
| (1)解:在长方体ABCD-A1B1C1D1中, 因为AB=1,E为AB的中点,所以,AE= 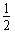 , ,又因为AD=2, 所以S△ADE= 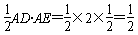 , ,又AA1⊥底面ABCD,AA1=2, 所以三棱锥A1-ADE的体积V=S△ADE·AA1= 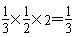 。 。(2)证明:因为AB⊥平面ADD1A1,A1D 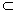 平面ADD1A1, 平面ADD1A1,所以AB⊥A1D, 因为ADD1A1为正方形,所以AD1⊥A1D, 又AD1∩AB=A,AD1 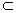 平面ABC1D1,AB 平面ABC1D1,AB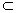 平面ABC1D1, 平面ABC1D1,所以A1D⊥平面ABC1D1。 |
|
| (3)证明:设AD1,A1D的交点为O,连结OE, 因为ADD1A1为正方形, 所以O是AD1的中点, 在△AD1B中,OE为中位线, 所以OE∥BD1, 又OE 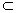 平面A1DE,BD1 平面A1DE,BD1 平面A1DE, 平面A1DE,所以BD1∥平面A1DE。 |
 |

练习册系列答案
相关题目
 19、如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点.
19、如图,长方体ABCD-A1B1C1D1中,AB=AD=1,AA1=2,点P为DD1的中点. 15、如图,长方体ABCD-A1B1C1D1中被截去一部分,
15、如图,长方体ABCD-A1B1C1D1中被截去一部分, 如图在长方体ABCD-A1B1C1D1中,其中AB=BC,E,F分别是AB1,BC1的中点,则以下结论中
如图在长方体ABCD-A1B1C1D1中,其中AB=BC,E,F分别是AB1,BC1的中点,则以下结论中 如图,长方体ABCD-A1B1C1D1中,P是线段AC的中点.
如图,长方体ABCD-A1B1C1D1中,P是线段AC的中点.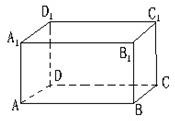 已知如图:长方体ABCD-A1B1C1D1中,交于顶点A的三条棱长别为AD=3,AA1=4,AB=5.一天,小强观察到在A处有一只蚂蚁,发现顶点C1处有食物,于是它沿着长方体的表面爬行去获取食物,则蚂蚁爬行的最短路程是( )
已知如图:长方体ABCD-A1B1C1D1中,交于顶点A的三条棱长别为AD=3,AA1=4,AB=5.一天,小强观察到在A处有一只蚂蚁,发现顶点C1处有食物,于是它沿着长方体的表面爬行去获取食物,则蚂蚁爬行的最短路程是( )