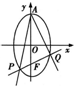Question

已知椭圆C：x2+

y2

4

=1，过点M（0，3）的直线l与椭圆C相交于不同的两点A、B．
（1）若l与x轴相交于点N，且A是MN的中点，求直线l的方程；
（2）设P为椭圆上一点，且

OA

+

OB

=λ

OP

（O为坐标原点），求当|AB|＜

3

时，实数λ的取值范围．

Answer 1

分析：（1）设A（x₁，y₁），因为A为MN的中点，且M的纵坐标为3，N的纵坐标为0，进而求得y_l，又根据点A在椭圆C上，
代入即可求得x₁，则点A的坐标可求．
（2）设直线AB的方程和点A，B，P的坐标，把直线方程与椭圆方程联立消去y，根据判别式大于0求得k的范围，根据韦达定理表示出x₁+x₂和x₁x₂，进而表示出AB的长度，求得k的范围，进而根据

OA

+

OB

=λ

OP

可知（x₁，y₁）十（x₂，y₂）=λ（x₃，y₃），进而分当λ≠0和λ=0时根据k的范围确定λ的取值范围．

解答：解：（1）设A（x₁，y₁），
因为A为MN的中点，且M的纵坐标为3，N的纵坐标为0，
所以y_l=

3

2

，
又因为点A（x_l，y_l）在椭圆C上，
所以x₁²+

y 2 1

4

=1，即

x

2 1

+

9

16

=1，解得x₁₌±

7

4

，
则点A的坐标为（

7

4

，

3

2

）或（-

7

4

，

3

2

），
所以直线l的方程为6

7

x-7y+21=0或6

7

x+7y-21=0．
（2）设直线AB的方程为y=kx+3或x=0，A（x₁，y₁），B（x₂，y₂），P（x₃，y₃），
当AB的方程为x=0时，|AB|=4＞

3

，与题意不符．
当AB的方程为y=kx+3时：
由题设可得A、B的坐标是方程组

y=kx+3 x2+ y2 4 =1

的解，
消去y得（4+k²）x²+6kx+5=0，
所以△=（6k）²-20（4+k²）＞0，即k²＞5，
则x₁+x₂=

-6k

4+k2

，x₁•x₂=

5

4+k2

，y₁+y₂=（kx₁+3）+（kx₂+3）=

24

4+k2

因为|AB|=

(x1-x2)2+(y1-y2)2

＜

3

，
所以

1+k2

•

( -6k 4+k2 )2- 20 4+k2

＜

3

，解得-

16

13

＜k²＜8
所以5＜k²＜8．
因为

OA

+

OB

=λ

OP

，即（x₁，y₁）十（x₂，y₂）=λ（x₃，y₃），
所以当λ=0时，由

OA

+

OB

=0，得x₁+x₂=

-6k

4+k2

=0，y₁+y₂=

24

4+k2

=0，
上述方程无解，所以此时符合条件的直线l不存在；
当λ≠0时，x₃=

x1+x2

λ

=-

-6k

λ(4+k2)

，y₃=

y1+y2

λ

=

24

λ(4+k2)

因为点P（x₃，y₃）在椭圆上，
所以[

-6k

λ(4+k2)

]²+

1

4

[

24

λ(4+k2)

]²=1化简得λ²=

36

4+k2

，
因为5＜k²＜8，所以3＜λ²＜4，
则λ∈（-2，-

3

）∪（

3

，2）．
综上，实数λ的取值范围为（-2，-

3

）∪（

3

，2）．

点评：本题主要考查了椭圆的简单性质，直线与椭圆的关系，解析几何的知识，解不等式．考查了学生综合分析问题和解决问题的能力．