题目内容

若两个非零向量
a
，
b
满足|
a
+
b
|=|
a
-
b
|=2|
a
|，则向量
b
与
a
+
b
的夹角为（　　）
分析：根据向量模的性质，建立关于
a
、
b
的方程组，解出
a
•
b
=0且
b
2=3
a
2．由此作出矩形OABC，可得
OC
=
OA
+
OB
=
a
+
b
，且|
OB
|=
3
|
OA
|．由此利用解三角形的知识，即可得到向量
b
与
a
+
b
的夹角大小．
解答：解：由已知得
(
a
+
b
)2=(
a
-
b
)2
(
a
-
b
)2=4
a
2
，化简①得
a
•
b
=0且
b
2=3
a
2．
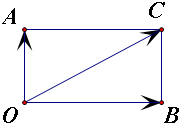
令
OA
=
a
，
OB
=
b
，
OC
=
OA
+
OB
=
a
+
b
，则
由
a
•
b
=0且
b
2=3
a
2，可得四边形OACB为矩形，且|
OB
|=
3
|
OA
|
∠BOC即为向量
b
与
a
+
b
的夹角．
令|
OA
|=1，则|
OB
|=
3

Rt△OBC中，tan∠BOC=
|BC|
|OB|
=
3
3
，
∴∠BOC=
π
6
，即向量
b
与
a
+
b
的夹角为
π
6

故选：A
点评：本题考查向量的数量积、模、夹角的运算．本题的关键是将已知转化，得出
a
、
b
的关系，属于中档题．
练习册系列答案
相关题目
在下列命题中：①若两个非零向量
a
和
b
共线，则
a
，
b
所在的直线平行；②若
a
，
b
所在的直线是异面直线，则
a
，
b
一定不共面；③若
a
，
b
，
c
三向量两两共面，则
a
，
b
，
c
c三直线一定也共面；其中正确命题的个数为（　　）
A、0B、1C、2D、3
在下列命题中：
①若两个非零向量
a
和
b
共线则
a
，
b
所在的直线平行；
②若
a
，
b
所在的直线是异面直线，则
a
，
b
一定不共面；
③若
a
，
b
，
c
三向量两两共面，则
a
，
b
，
c
三向量一定也共面；
④若
a
，
b
，
c
是三个非零向量，则空间任意一个向量p总可以唯一表示为
p
=x
a
+y
b
+z
c
（x，y，z∈R）．
其中正确命题的个数为（　　）
A、0B、1C、2D、3
（2013•青岛一模）若两个非零向量
a
，
b
满足|
a
+
b
|+|
a
-
b
|=2|
a
|，则向量
a
+
b
与
b
-
a
的夹角为（　　）
（2013•丽水一模）若两个非零向量
a
，
b
满足|
a
+
b
|=|
a
-
b
|=2|
a
|，则向量
a
与
a
+
b
的夹角是
π
3
π
3
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网