题目内容
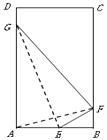
【题目】如图,四边形ABCD中,△BCD为正三角形,AD=AB=2, ![]() ,AC与BD中心O点,将△ACD沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为60°.
,AC与BD中心O点,将△ACD沿边AC折起,使D点至P点,已知PO与平面ABCD所成的角为60°. 
(1)求证:平面PAC⊥平面PDB;
(2)求已知二面角A﹣PB﹣D的余弦值.
【答案】
(1)解:证明:∵△BCD为正三角形,AD=AB=2,易知O为BD的中点,则AC⊥BD,
又PO平面PBD,所以AC⊥平面PBD,∵AC平面PAC,∴平面PAC⊥平面PD B.
(2)解:过P作DB的垂线,垂足为H,则PH垂直平面ABCD,∠PHO=60°,
以OB为x后,OC为y轴,过O垂直于平面ABC向上的直线为z轴建立如图所示空间直角坐标系,
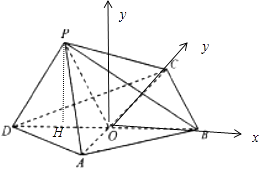
则A(0,﹣1,0), ![]() ,
, ![]() ,
,
易知平面PBD的法向量为 ![]() ,
, ![]() ,
, ![]() ,
,
设平面ABP的法向量为 ![]() ,
,
则由 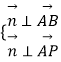 得
得 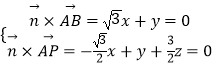 ,
,
取 ![]() ,
, ![]() ,
,
二面角A﹣PB﹣D的余弦值为 ![]() .
.
【解析】(1)易知O为BD的中点,则AC⊥BD,即AC⊥平面PBD,即平面PAC⊥平面PDB.(2)过P作DB的垂线,垂足为H,则PH垂直平面ABCD,∠PHO=60°,以OB为x后,OC为y轴,过O垂直于平面ABC向上的直线为z轴建立如图所示空间直角坐标系,利用向量法求解.
【考点精析】掌握平面与平面垂直的判定是解答本题的根本,需要知道一个平面过另一个平面的垂线,则这两个平面垂直.

练习册系列答案
相关题目