题目内容
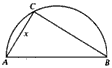
 两城市A和B相距20km,现计划在两城市外以AB为直径的半圆弧
两城市A和B相距20km,现计划在两城市外以AB为直径的半圆弧 上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k,当垃圾处理厂建在
上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的距离有关,对城A和城B的总影响度为城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k,当垃圾处理厂建在 的中点时,对城A和城B的总影响度为0.065.
的中点时,对城A和城B的总影响度为0.065.
(1)将y表示成x的函数;
(2)判断弧 上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由.
上是否存在一点,使建在此处的垃圾处理厂对城A和城B的总影响度最小?若存在,求出该点到城A的距离;若不存在,说明理由.
解:(1)由题意得 ,
,
又∵当 时,y=0.065,
时,y=0.065,
∴k=9
∴ (7分)
(7分)
(2) ,
,
令t=x2+320∈(320,720),
则 ,当且仅当
,当且仅当 时,等号成立.(14分)
时,等号成立.(14分)
∴弧 上存在一点,该点到城A的距离为
上存在一点,该点到城A的距离为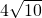 时,使建在此处的垃圾处理厂对城A和城B的总影响度最小为0.0625.(16分)
时,使建在此处的垃圾处理厂对城A和城B的总影响度最小为0.0625.(16分)
分析:(1)根据“垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k,”建立函数模型: ,再根据当
,再根据当 时,y=0.065,求得参数k.
时,y=0.065,求得参数k.
(2)总影响度最小,即为:求 的最小值时的状态.令t=x2+320,将函数转化为:
的最小值时的状态.令t=x2+320,将函数转化为: ,再用基本不等式求解.
,再用基本不等式求解.
点评:本题主要考查函数模型的建立和应用,主要涉及了换元法,基本不等式法和转化思想的考查.
 ,
,又∵当
 时,y=0.065,
时,y=0.065,∴k=9
∴
 (7分)
(7分)(2)
 ,
,令t=x2+320∈(320,720),
则
 ,当且仅当
,当且仅当 时,等号成立.(14分)
时,等号成立.(14分)∴弧
 上存在一点,该点到城A的距离为
上存在一点,该点到城A的距离为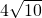 时,使建在此处的垃圾处理厂对城A和城B的总影响度最小为0.0625.(16分)
时,使建在此处的垃圾处理厂对城A和城B的总影响度最小为0.0625.(16分)分析:(1)根据“垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k,”建立函数模型:
 ,再根据当
,再根据当 时,y=0.065,求得参数k.
时,y=0.065,求得参数k.(2)总影响度最小,即为:求
 的最小值时的状态.令t=x2+320,将函数转化为:
的最小值时的状态.令t=x2+320,将函数转化为: ,再用基本不等式求解.
,再用基本不等式求解.点评:本题主要考查函数模型的建立和应用,主要涉及了换元法,基本不等式法和转化思想的考查.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
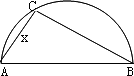
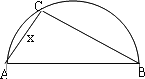
 上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的距离有关,对城A和城B的总影响度为对城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k,当垃圾处理厂建在
上选择一点C建造垃圾处理厂,其对城市的影响度与所选地点到城市的距离有关,对城A和城B的总影响度为对城A与城B的影响度之和,记C点到城A的距离为x km,建在C处的垃圾处理厂对城A和城B的总影响度为y,统计调查表明:垃圾处理厂对城A的影响度与所选地点到城A的距离的平方成反比,比例系数为4;对城B的影响度与所选地点到城B的距离的平方成反比,比例系数为k,当垃圾处理厂建在 的中点时,对城A和城B的总影响度为0.065,
的中点时,对城A和城B的总影响度为0.065,