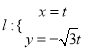Question

【题目】选修4-4：坐标系与参数方程

在直角坐标系中，直线的参数方程为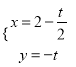，（ 为参数），在以坐标原点为极点， 轴正半轴为极轴的极坐标系中，曲线的极坐标方程为

（Ⅰ）求直线的普通方程和曲线的直角坐标方程；

（Ⅱ）已知点，若点是直线上一动点，过点作曲线的两条切线，切点分别为，求四边形面积的最小值.

Answer 1

【答案】（Ⅰ）（Ⅱ）2

【解析】试题分析：（1）利用三种方程的转化方法，可得直线的普通方程和曲线的直角坐标方程；（2）利用切线的几何性质，将四边形面积为直角三角形的面积问题.

试题解析：

（Ⅰ）由得，代入化简得，

因为，所以，

又因为，所以

所以直线的普通方程为，曲线的直角坐标方程为；

（Ⅱ）将化为，得点恰为该圆的圆心.

设四边形的面积为，则，当最小时， 最小，

而的最小值为点到直线的距离

所以