题目内容
已知数列{an}与{bn}满足: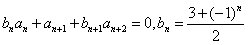 ,n∈N*,且a1=2,a2=4,
,n∈N*,且a1=2,a2=4,
(Ⅰ)求a3,a4,a5的值;
(Ⅱ)设cn=a2n-1+a2n+1,n∈N*,证明:{cn}是等比数列;
(Ⅲ)设Sk=a2+a4+…+a2k,k∈N*,证明: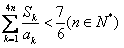 .
.
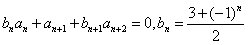 ,n∈N*,且a1=2,a2=4,
,n∈N*,且a1=2,a2=4,(Ⅰ)求a3,a4,a5的值;
(Ⅱ)设cn=a2n-1+a2n+1,n∈N*,证明:{cn}是等比数列;
(Ⅲ)设Sk=a2+a4+…+a2k,k∈N*,证明:
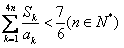 .
. (Ⅰ)解:由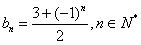 ,可得
,可得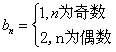 ,
,
又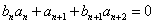 ,
,
当n=1时,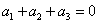 ,由
,由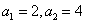 ,可得
,可得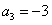 ;
;
当n=2时,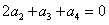 ,可得
,可得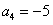 ;
;
当n=3时,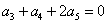 ,可得
,可得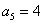 。
。
(Ⅱ)证明:对任意n∈N*,
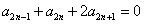 , ①
, ①
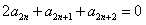 , ②
, ②
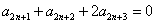 , ③
, ③
②-③,得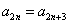 , ④
, ④
将④代入①,可得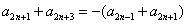 ,
,
即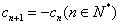 ,
,
又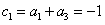 ,
,
故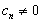 ,
,
因此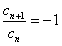 ,所以{cn}是等比数列。
,所以{cn}是等比数列。
(Ⅲ)证明:由(Ⅱ)可得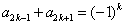 ,
,
于是,对任意k∈N*且k≥2,有
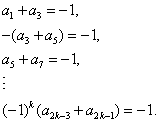
将以上各式相加,得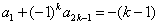 ,
,
即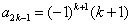 ,
,
此式当k=1时也成立;
由④式得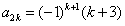 ,
,
从而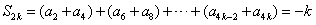 ,
,
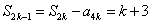 ,
,
所以,对任意n∈N*,n≥2,
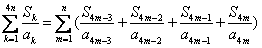
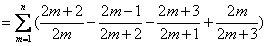
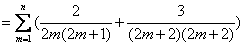
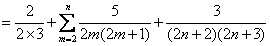
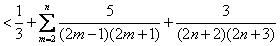
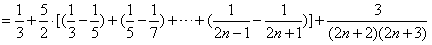
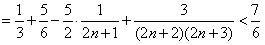 ,
,
对于n=1,不等式显然成立。
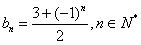 ,可得
,可得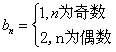 ,
,又
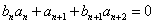 ,
,当n=1时,
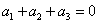 ,由
,由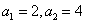 ,可得
,可得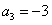 ;
;当n=2时,
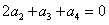 ,可得
,可得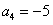 ;
;当n=3时,
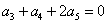 ,可得
,可得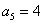 。
。(Ⅱ)证明:对任意n∈N*,
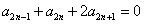 , ①
, ① 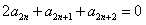 , ②
, ②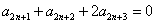 , ③
, ③②-③,得
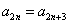 , ④
, ④ 将④代入①,可得
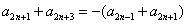 ,
,即
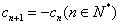 ,
,又
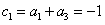 ,
,故
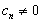 ,
,因此
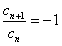 ,所以{cn}是等比数列。
,所以{cn}是等比数列。(Ⅲ)证明:由(Ⅱ)可得
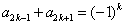 ,
,于是,对任意k∈N*且k≥2,有
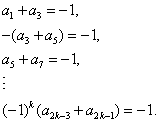
将以上各式相加,得
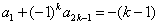 ,
,即
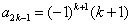 ,
,此式当k=1时也成立;
由④式得
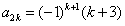 ,
,从而
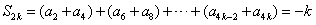 ,
,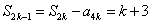 ,
,所以,对任意n∈N*,n≥2,
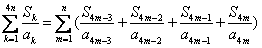
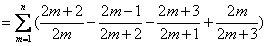
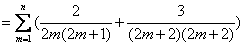
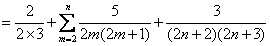
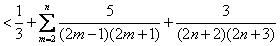
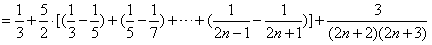
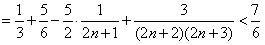 ,
,对于n=1,不等式显然成立。

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
