题目内容

函数f（x）=|x|•（|x|+|2-x|）-1有
2
2
个零点．
分析：要求函数f（x）=|x|•（|x|+|2-x|）-1，可以分别画出y=
1
|x|
与y=|x|+|2-x|的图象，看其有几个交点，即可求解；
解答：解：∵函数f（x）=|x|•（|x|+|2-x|）-1，
令y=
1
|x|
与y=|x|+|2-x|，y=
1
|x|
为偶函数，
y=|x|+|2-x|=
2x-2，x＞2
2，0＜x＜2
-2x+2，x＜0
；
分别画出这两个函数如下图：

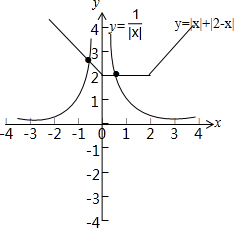
y=
1
|x|
与y=|x|+|2-x|的图象有两个交点，
∴函数f（x）=|x|•（|x|+|2-x|）-1有2个零点；
故答案为2；
点评：本题考查函数的零点有数形结合的数学思想方法，数形结合是数学解题中常用的思想方法，能够变抽象思维为形象思维，有助于把握数学问题的本质．
练习册系列答案
相关题目
设函数f（x）=a2x2（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为
2
，求a的值；
（2）关于x的不等式（x-1）2＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=
2
2
，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．
（2012•深圳一模）已知函数f(x)=
1
3
x3+bx2+cx+d，设曲线y=f（x）在与x轴交点处的切线为y=4x-12，f′（x）为f（x）的导函数，且满足f′（2-x）=f′（x）．
（1）求f（x）；
（2）设g(x)=x
f′(x)
 ， m＞0，求函数g（x）在[0，m]上的最大值；
（3）设h（x）=lnf′（x），若对一切x∈[0，1]，不等式h（x+1-t）＜h（2x+2）恒成立，求实数t的取值范围．
（2011•上海模拟）已知函数f(x)=(
x
a
-1)2+(
b
x
-1)2，x∈(0，+∞)，其中0＜a＜b．
（1）当a=1，b=2时，求f（x）的最小值；
（2）若f（a）≥2m-1对任意0＜a＜b恒成立，求实数m的取值范围；
（3）设k、c＞0，当a=k2，b=（k+c）2时，记f（x）=f1（x）；当a=（k+c）2，b=（k+2c）2时，记f（x）=f2（x）．
求证：f1(x)+f2(x)＞
4c2
k(k+c)
．
已知函数f(x)=
1
3
x3+bx2+cx+d，设曲线y=f（x）在与x轴交点处的切线为y=4x-12，f′（x）为f（x）的导函数，且满足f′（2-x）=f′（x）．
（1）求f（x）；
（2）设g(x)=x
f′(x)
 ， m＞0，求函数g（x）在[0，m]上的最大值；
（3）设h（x）=lnf′（x），若对一切x∈[0，1]，不等式h（x+1-t）＜h（2x+2）恒成立，求实数t的取值范围．
设函数f（x）=a2x2（a＞0），g（x）=blnx．
（1）若函数y=f（x）图象上的点到直线x-y-3=0距离的最小值为2
2
，求a的值；
（2）关于x的不等式（x-1）2＞f（x）的解集中的整数恰有3个，求实数a的取值范围；
（3）对于函数f（x）与g（x）定义域上的任意实数x，若存在常数k，m，使得f（x）≥kx+m和g（x）≤kx+m都成立，则称直线y=kx+m为函数f（x）与g（x）的“分界线”．设a=
2
2
，b=e，试探究f（x）与g（x）是否存在“分界线”？若存在，求出“分界线”的方程；若不存在，请说明理由．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网