题目内容
下列命题中所有假命题的序号为______.
①y=sinxcosx的周期为π,最大值为
; ②若x是第一象限的角,则y=sinx是增函数;③在△ABC中,若sinA=sinB,则A=B; ④f(x)=sinx+cosx既不是奇函数,也不是偶函数; ⑤y=cos(2x+
)的一条对称轴为x=-
.
①y=sinxcosx的周期为π,最大值为
| 1 |
| 2 |
| π |
| 4 |
| π |
| 8 |
①y=sinxcosx=
sin2x,
∵ω=2,∴T=
=π,
又sin2x∈[-1,1],
∴函数的最大值为
,本选项为真命题;
②由于390°>30°,且都是第一象限角,sin390°=sin30°=
,
故函数y=sinx在第一象限不是增函数,本选项为假命题;
③在△ABC中,若sinA=sinB,得到A=B或A+B=π(舍去),
∴A=B,本选项为真命题;
④f(x)=sinx+cosx=
sin(x+
),
∵正弦函数sin(x+
)为奇函数,
∴函数f(x)=sinx+cosx为奇函数,本选项为假命题;
⑤y=cos(2x+
),
令2x+
=kπ,解得x=
-
,
当k=0时,函数的对称轴为x=-
,
∴函数的一条对称轴为x=-
,本选项为真命题,
故答案为:②④
| 1 |
| 2 |
∵ω=2,∴T=
| 2π |
| 2 |
又sin2x∈[-1,1],
∴函数的最大值为
| 1 |
| 2 |
②由于390°>30°,且都是第一象限角,sin390°=sin30°=
| 1 |
| 2 |
故函数y=sinx在第一象限不是增函数,本选项为假命题;
③在△ABC中,若sinA=sinB,得到A=B或A+B=π(舍去),
∴A=B,本选项为真命题;
④f(x)=sinx+cosx=
| 2 |
| π |
| 4 |
∵正弦函数sin(x+
| π |
| 4 |
∴函数f(x)=sinx+cosx为奇函数,本选项为假命题;
⑤y=cos(2x+
| π |
| 4 |
令2x+
| π |
| 4 |
| kπ |
| 2 |
| π |
| 8 |
当k=0时,函数的对称轴为x=-
| π |
| 8 |
∴函数的一条对称轴为x=-
| π |
| 8 |
故答案为:②④

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
 ; ②若x是第一象限的角,则y=sinx是增函数;③在△ABC中,若sinA=sinB,则A=B; ④f(x)=sinx+cosx既不是奇函数,也不是偶函数; ⑤
; ②若x是第一象限的角,则y=sinx是增函数;③在△ABC中,若sinA=sinB,则A=B; ④f(x)=sinx+cosx既不是奇函数,也不是偶函数; ⑤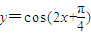 的一条对称轴为
的一条对称轴为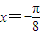 .
. 的否定是
的否定是 ;
; 前
前 项和为
项和为 ,则三点
,则三点 共线;
共线; 上单调递减;
上单调递减; 中,若
中,若 则
则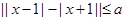 恒成立,则实数
恒成立,则实数 的取值范围是
的取值范围是 。
。