题目内容
已知复数z1,z2满足|z1|=|z2|=1,且
(1)求|z1-z2|的值;
(2)求证: ;
;
解:(1)由条件|z1-z2|= ,可记复数z的共轭复数为
,可记复数z的共轭复数为 .
.
∵|z1|=|z2|=1.∴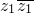 =
= =1.
=1.
又|z1+z2|= ,∴(z1+z2)
,∴(z1+z2) =2.═>
=2.═>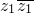 +
+ +(
+( +
+ )=2.
)=2.
═> +
+ =0.
=0.
∴|z1-z2|2=(z1-z2) =
=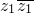 +
+ +(
+( +
+ )=2.
)=2.
∴|z1-z2|=
(2)∵|Z1+Z2|=|Z1-Z2|
∴|Z1+Z2|2=|Z1-Z2|2
∴(z1+z2) =(z1-z2)
=(z1-z2)
∴ =-
=-
∴
∴ 是纯虚数,∴
是纯虚数,∴
分析:(1)利用共轭复数与复数的模相等,|z|| |=z2=
|=z2= ,求出|z1-z2|2的值,进而确定|z1-z2|的值.
,求出|z1-z2|2的值,进而确定|z1-z2|的值.
(2)利用(1)的(z1+z2) =(z1-z2)
=(z1-z2) ,推出
,推出 =-
=- ,确定
,确定 是纯虚数,得到要证明的结论.
是纯虚数,得到要证明的结论.
点评:本题考查复数求模,复数的基本概念,考查计算能力,是基础题,公式的灵活运用,是解好题目的关键.
 ,可记复数z的共轭复数为
,可记复数z的共轭复数为 .
.∵|z1|=|z2|=1.∴
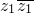 =
= =1.
=1.又|z1+z2|=
 ,∴(z1+z2)
,∴(z1+z2) =2.═>
=2.═>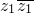 +
+ +(
+( +
+ )=2.
)=2.═>
 +
+ =0.
=0.∴|z1-z2|2=(z1-z2)
 =
=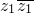 +
+ +(
+( +
+ )=2.
)=2.∴|z1-z2|=

(2)∵|Z1+Z2|=|Z1-Z2|
∴|Z1+Z2|2=|Z1-Z2|2
∴(z1+z2)
 =(z1-z2)
=(z1-z2)
∴
 =-
=-
∴

∴
 是纯虚数,∴
是纯虚数,∴
分析:(1)利用共轭复数与复数的模相等,|z||
 |=z2=
|=z2= ,求出|z1-z2|2的值,进而确定|z1-z2|的值.
,求出|z1-z2|2的值,进而确定|z1-z2|的值.(2)利用(1)的(z1+z2)
 =(z1-z2)
=(z1-z2) ,推出
,推出 =-
=- ,确定
,确定 是纯虚数,得到要证明的结论.
是纯虚数,得到要证明的结论.点评:本题考查复数求模,复数的基本概念,考查计算能力,是基础题,公式的灵活运用,是解好题目的关键.

练习册系列答案
相关题目