题目内容
如图,直三棱柱(侧棱垂直于底面的棱柱) ,底面
,底面 中
中 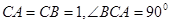 ,棱
,棱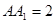 ,
,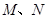 分别为
分别为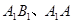 的中点.
的中点.
(1)求 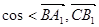 >的值;
>的值;
(2)求证:
(3)求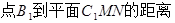 .
.
(1) ;(2)只需证
;(2)只需证 ;(3)
;(3) 。
。
解析试题分析:以C为原点,CA、CB、CC1所在的直线分别为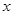 轴、
轴、 轴、
轴、 轴,建立如图所示的坐标系
轴,建立如图所示的坐标系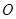 -
-
(1)依题意得 ,
,
∴
∴
 ,
,
∴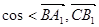 >=
>=
(2) 依题意得 ∴
∴ ,
,
∴ ,
, ,
,
∴

∴ ,
,
∴
∴ (Ⅲ)
(Ⅲ)
考点:异面直线所成的角;线面垂直的判定定理;点到平面的距离。
点评:①本题主要考查了空间的线面垂直的证明以及异面直线所成的角、点到平面的距离,充分考查了学生的逻辑推理能力,空间想象力,以及识图能力。②我们要熟练掌握正棱柱、直棱柱的结构特征。正棱柱:底面是正多边形,侧棱垂直底面。直棱柱:侧棱垂直底面。

练习册系列答案
 走进文言文系列答案
走进文言文系列答案
相关题目
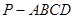 中,底面ABCD是正方形,侧棱
中,底面ABCD是正方形,侧棱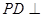 底面ABCD,
底面ABCD,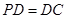 ,E是PC的中点,作
,E是PC的中点,作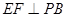 交PB于点F.
交PB于点F.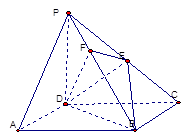

 BCD=60
BCD=60 ,E是CD的中点,PA
,E是CD的中点,PA 底面ABCD,PA=2.
底面ABCD,PA=2.
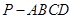 中,
中,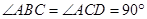 ,
,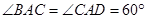 ,
, 平面
平面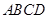 ,
,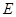 为
为 的中点,
的中点, .
.
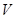 ;
;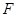 为
为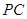 的中点,求证:平面
的中点,求证:平面 平面
平面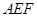 ;
;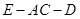 的大小。.
的大小。. ,求AB1与C1B所成角的大小。
,求AB1与C1B所成角的大小。
 ,E、F分别是AB、PD的中点.
,E、F分别是AB、PD的中点.
 平面PCD;
平面PCD; 中.
中.
 与
与 所成的角;
所成的角; ⊥平面
⊥平面 .
. 分别是
分别是 中点)
中点)
 平面
平面 ;
; 的体积.
的体积.