题目内容
选修4－1几何证明选讲
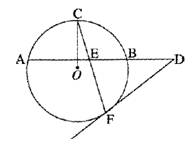
如图，在Rt△ABC中，∠C＝90°，BE平分∠ABC交AC于点E，点D在AB上，DE⊥EB．
(1)求证：AC是△BDE的外接圆的切线；
(2)若AD＝2
，AE＝6，求EC的长．
答案：
解析：
解析：
|
解：(1)取BD的中点O，连接OE． ∵BE平分∠ABC，∴∠CBE＝∠OBE． 又∵OB＝OE，∴∠OBE＝∠BEO， ∴∠CBE＝∠BEO，∴BC∥OE． 3分 ∵∠C＝90°，∴OE⊥AC，∴AC是△BDE的外接圆的切线． 5分 (2)设⊙O的半径为r，则在△AOE中， 解得 ∴OA＝2OE，∴∠A＝30°，∠AOE＝60°． ∴∠CBE＝∠OBE＝30°． ∴EC＝ |
，即
， 7分
． 10分
练习册系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案
小学暑假作业东南大学出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案
相关题目
的半圆O上一点，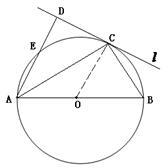
（选修4－1 几何证明选讲）（本题满分10分）
,
为圆周上一点，
,过
，过A作
的度数与线段AE的长。
内接于
，
，直线
切
交
于点
.若
则
的长为 ．
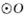的弦，C、F是
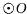上的点，OC垂直于弦AB，过点F作
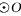的切线，交AB的延长线于D，连结CF交AB于点E.
；
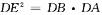，且AE=2，则AC= ； 