题目内容
现有m(m≥2)个不同的数P1、P2、P3、…、Pn.将他们按一定顺序排列成一列.对于其中的两项Pi和Pj,若满足:1≤i<j≤m且Pi>Pj(即前面某数大于后面某数),则称Pi与Pj构成一个逆序.一个排列的全部逆序的总数称为该排列的逆序数.记排列(n+1)、n、(n-1)、…3、2、1的逆序数为an.如排列2、1的逆序数a1=1,排列3、2、1的逆序数a2=3.
(1)求a3、a4、a5;
(2)求an的表达式;
(3)令bn=
+
,证明b1+b2+…bn<2n+3,n=1,2,….
(1)求a3、a4、a5;
(2)求an的表达式;
(3)令bn=
| an |
| an+1 |
| an+1 |
| an |
(I)由已知得a3=6,a4=10,a5=15,
(II)∵a1=1,
a2=3=2+1,
a3=6=3+2+1,
a4=10=4+3+2+1,
a5=15=5+4+3+2+1,
…
∴不妨猜想an=n+(n-1)+…+2+1=
(III)因为an=n+(n-1)+…+2+1=
,
又因为bn=
+
=2+
-
,n=1,2,,
所以b1+b2+…+bn=2n+2[(1-
)+(
-
)+…+(
-
)]
=2n+3-
-
<2n+3.
综上,b1+b2+…+bn<2n+3,n=1,2,.
(II)∵a1=1,
a2=3=2+1,
a3=6=3+2+1,
a4=10=4+3+2+1,
a5=15=5+4+3+2+1,
…
∴不妨猜想an=n+(n-1)+…+2+1=
| n(n+1) |
| 2 |
(III)因为an=n+(n-1)+…+2+1=
| n(n+1) |
| 2 |
又因为bn=
| n |
| n+2 |
| n+2 |
| n |
| 2 |
| n |
| 2 |
| n+2 |
所以b1+b2+…+bn=2n+2[(1-
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| n |
| 1 |
| n+2 |
=2n+3-
| 2 |
| n+1 |
| 2 |
| n+2 |
综上,b1+b2+…+bn<2n+3,n=1,2,.

练习册系列答案
相关题目
 与
与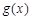 ,如果对任意
,如果对任意 ,均有
,均有 与
与 (a > 0且
(a > 0且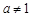 ),给定区间
),给定区间 .
. 与
与 在给定区间
在给定区间 与
与 ,如果对任意
,如果对任意 ,均有
,均有 ,则称
,则称 与
与 (a > 0且
(a > 0且 ),给定区间
),给定区间 .
. 与
与 在给定区间
在给定区间