题目内容
直线l过点M(2,1),且分别交x轴、y轴的正半轴于点A、B.点O是坐标原点.
(1) 当△ABO的面积最小时,求直线l的方程;
(2) 当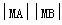 最小时,求直线l的方程.
最小时,求直线l的方程.
解:(1) 如图,设 =a,
=a, =b,△ABO的面积为S,则S=
=b,△ABO的面积为S,则S= ab,并且直线l的截距式方程是
ab,并且直线l的截距式方程是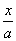 +
+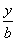 =1,
=1,
由直线通过点(2,1),得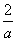 +
+ =1,
=1,
所以 =
= =
= .
.
因为A点和B点在x轴、y轴的正半轴上,所以上式右端的分母b-1>0.由此得
S= ×b=
×b= ×b=
×b= =b+1+
=b+1+
=b-1+ +2≥2+2=4.
+2≥2+2=4.
当且仅当b-1= ,即b=2时,面积S取最小值4,这时a=4,直线的方程为
,即b=2时,面积S取最小值4,这时a=4,直线的方程为 +
+ =1.
=1.
即直线l的方程为x+2y-4=0.

(2) 如上图,设∠BAO=θ,则 =
= ,
, =
= ,
,
所以
 =
=
当θ=45°时 有最小值4,此时直线斜率为-1,∴直线l的方程为x+y-3=0.
有最小值4,此时直线斜率为-1,∴直线l的方程为x+y-3=0.

练习册系列答案
相关题目
 D.
D. ,P(B)=
,P(B)= ,则x+y的最小值为( )
,则x+y的最小值为( ) :
: 的焦距为
的焦距为 ,离心率为
,离心率为 ,其右焦点为
,其右焦点为 ,过点
,过点 作直线交椭圆于另一点
作直线交椭圆于另一点 .
. ,求
,求 外接圆的方程;
外接圆的方程; 的直线与椭圆
的直线与椭圆
 相交于两点
相交于两点 、
、 ,设
,设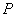 为
为 上一点,且满足
上一点,且满足 (
( 为坐标原点),当
为坐标原点),当 时,求实数
时,求实数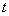 的取值范围.
的取值范围. 的反函数
的反函数 则
则 B.
B. C.
C. D.
D.
 ,点
,点 在曲线
在曲线 上,若阴影部分面积与△
上,若阴影部分面积与△ 面积相等时,则
面积相等时,则 .
. 