题目内容
已知函数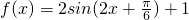 .
.
(1)求f(x)的最小正周期及振幅;
(2)试判断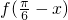 与
与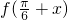 的大小关系,并说明理由.
的大小关系,并说明理由.
(3)若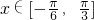 ,求f(x)的最大值和最小值.
,求f(x)的最大值和最小值.
解:(1)f(x)的最小正周期为 ,振幅A=2
,振幅A=2
(2)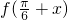 =
=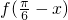
法一:因为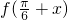 =
=
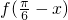 =
=
所以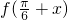 =
=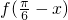
法二:因为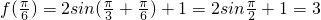 为函数的最大值,
为函数的最大值,
所以 是函数的一条对称轴,所以
是函数的一条对称轴,所以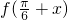 =
=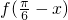 .
.
(2)∵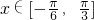
∴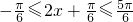
∴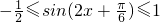
∴ ,
,
∴0≤f(x)≤3
∴f(x)的最小值为0; f(x)的最大值为3.
分析:(1)由y=Asin(ωx+φ)型函数中参数的几何意义及周期计算公式,即可得f(x)的最小正周期及振幅;(2)可以利用诱导公式分别化简两个函数式来进行证明,也可先证明 是函数的一条对称轴,从而证明两式相等;(3)先求内层函数的值域,再利用正弦函数的图象求函数f(x)在
是函数的一条对称轴,从而证明两式相等;(3)先求内层函数的值域,再利用正弦函数的图象求函数f(x)在 上的最大值和最小值
上的最大值和最小值
点评:本题考查了y=Asin(ωx+φ)型函数的图象和性质,函数的对称性和函数值域的求法,正弦函数的图象和性质及诱导公式的应用
 ,振幅A=2
,振幅A=2(2)
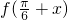 =
=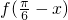
法一:因为
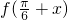 =
=
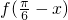 =
=
所以
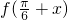 =
=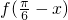
法二:因为
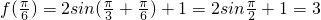 为函数的最大值,
为函数的最大值,所以
 是函数的一条对称轴,所以
是函数的一条对称轴,所以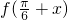 =
=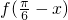 .
.(2)∵
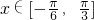
∴
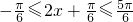
∴
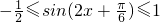
∴
 ,
,∴0≤f(x)≤3
∴f(x)的最小值为0; f(x)的最大值为3.
分析:(1)由y=Asin(ωx+φ)型函数中参数的几何意义及周期计算公式,即可得f(x)的最小正周期及振幅;(2)可以利用诱导公式分别化简两个函数式来进行证明,也可先证明
 是函数的一条对称轴,从而证明两式相等;(3)先求内层函数的值域,再利用正弦函数的图象求函数f(x)在
是函数的一条对称轴,从而证明两式相等;(3)先求内层函数的值域,再利用正弦函数的图象求函数f(x)在 上的最大值和最小值
上的最大值和最小值点评:本题考查了y=Asin(ωx+φ)型函数的图象和性质,函数的对称性和函数值域的求法,正弦函数的图象和性质及诱导公式的应用

练习册系列答案
 小夫子全能检测系列答案
小夫子全能检测系列答案
相关题目
 .
. .
. 的图象在x轴上方?
的图象在x轴上方? .
. 为f(x)的一个零点,求sin2x的值.
为f(x)的一个零点,求sin2x的值.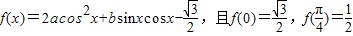 .
. .
. ,求f(x)的最大值和最小值.
,求f(x)的最大值和最小值.