题目内容
已知函数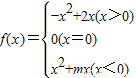 为奇函数.
为奇函数.(I)求实数m的值;
(II)求使f(x)=-1成立的x值.
【答案】分析:(I)设x<0,则-x>0,利用x>0时的解析式,结合函数是奇函数,求得x<0时的解析式,即可求得m的值;
(II)利用分段函数,建立方程,即可求得x的值.
解答:解:(I)设x<0,则-x>0,∴f(-x)=-x2-2x
∵函数是奇函数,∴f(x)=-f(-x)=x2+2x(x<0)
∴m=2;
(II)x>0时,-x2+2x=-1,∴x2-2x-1=0,
∴x=1+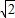 或x=1-
或x=1-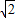 (舍去);
(舍去);
x<0时,x2+2x=-1,
∴x2+2x+1=0,
∴x=-1
故答案为:1+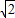 或-1.
或-1.
点评:本题考查函数的奇偶性,考查函数解析式的确定,考查求函数值,属于中档题.
(II)利用分段函数,建立方程,即可求得x的值.
解答:解:(I)设x<0,则-x>0,∴f(-x)=-x2-2x
∵函数是奇函数,∴f(x)=-f(-x)=x2+2x(x<0)
∴m=2;
(II)x>0时,-x2+2x=-1,∴x2-2x-1=0,
∴x=1+
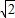 或x=1-
或x=1-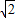 (舍去);
(舍去);x<0时,x2+2x=-1,
∴x2+2x+1=0,
∴x=-1
故答案为:1+
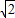 或-1.
或-1.点评:本题考查函数的奇偶性,考查函数解析式的确定,考查求函数值,属于中档题.

练习册系列答案
相关题目
 为奇函数,
为奇函数, 为偶函数,且
为偶函数,且 .
. ,则称
,则称 是函数
是函数 为奇函数,
为奇函数, 为偶函数
为偶函数 ,且
,且 .
. ,则称
,则称 是函数
是函数