题目内容
在⊿ABC中,BC=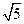 ,AC=3,sinC=2sinA
,AC=3,sinC=2sinA
(I) 求AB的值:
(II) 求sin 的值
的值
(Ⅰ)解:在△ABC中,根据正弦定理,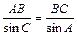

于是AB=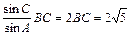
(Ⅱ)解:在△ABC中,根据余弦定理,得cosA=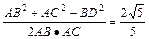
于是 sinA=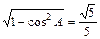
从而sin2A=2sinAcosA=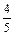 ,cos2A=cos2A-sin2A=
,cos2A=cos2A-sin2A=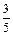

所以 sin(2A-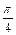 )=sin2Acos
)=sin2Acos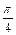 -cos2Asin
-cos2Asin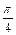 =
=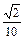
解析

练习册系列答案
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案
相关题目
 北偏东
北偏东 方向的点
方向的点 处有一观测站,港口正东方向的
处有一观测站,港口正东方向的 处有一轮船,测得
处有一轮船,测得 为
为 海里. 该轮船从
海里. 该轮船从 海里后到达
海里后到达 处,测得
处,测得 为
为 海里. 问此时轮船离港口
海里. 问此时轮船离港口
 中,
中, 是
是 的中点,
的中点, 是
是 的中点,
的中点, 的延长线交
的延长线交 于
于 .
.
 的值;
的值; 的面积为
的面积为 ,四边形
,四边形 的面积为
的面积为 ,求
,求 的值.
的值. 中,角A、B、C的对边分别为a、b、c,已知
中,角A、B、C的对边分别为a、b、c,已知 ,
, ,求b边的长。
,求b边的长。

 (
( ),且函数
),且函数 的最小正周期为
的最小正周期为 .
. 中,角
中,角 所对的边分别为
所对的边分别为 .若
.若 ,
, ,且
,且 ,试求
,试求 的值.
的值. 中,角A、B、C所对边分别是a、b、c,
中,角A、B、C所对边分别是a、b、c,
 ,求
,求 .
. 中,角
中,角 所列边分别为
所列边分别为 ,且
,且

 ;
; ,试判断
,试判断 取得最大值时
取得最大值时 ,
, ,其中0<
,其中0< <
< .
. =
= ,求角
,求角 的面积为
的面积为 ,求
,求 的值
的值 .
. 的长;
的长; 是
是 的中点,求中线
的中点,求中线 的长度.
的长度.