题目内容
【题目】设正项等差数列![]() 的前n项和为
的前n项和为![]() ,已知
,已知![]() 且
且![]() 成等比数列
成等比数列
(1)求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,求数列
,求数列![]() 的前n项和;
的前n项和;
(3)设数列![]() 满足
满足![]() 求证:
求证:![]()
【答案】(1) ![]() (2) 数列
(2) 数列![]() 的前n项和为
的前n项和为 (3)证明见解析.
(3)证明见解析.
【解析】
(1)等差数列![]() 的首项为
的首项为![]() ,公差为
,公差为![]() ,由条件可得
,由条件可得![]() ,
,![]() ,即
,即![]() ,两式联立可得:
,两式联立可得:![]() ,或
,或![]() ,经检验
,经检验![]() 满足条件.
满足条件.
(2)设![]() ,可得当
,可得当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,则当
,则当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,分情况求和即可.
,分情况求和即可.
(3) 由(1)有![]() ,由
,由![]() 有
有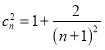 ,则则
,则则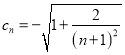 或
或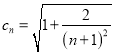 ,若
,若 则不等式
则不等式![]() 显然成立. 若
显然成立. 若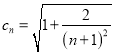 ,则
,则![]() ,由裂项相消法求和可证明.
,由裂项相消法求和可证明.
(1)等差数列![]() 的首项为
的首项为![]() ,公差为
,公差为![]() ,
,
由![]() 有
有![]() ,即
,即![]() …… ①
…… ①
由![]() 成等比数列,有
成等比数列,有![]() ,即
,即![]() ……②
……②
将①代入②得:![]()
即![]() 解得:
解得:![]() ,或
,或![]() .
.
当![]() 时,
时,![]() 与题目矛盾,舍去.
与题目矛盾,舍去.
当![]() 时,
时,![]() ,满足条件,此时
,满足条件,此时![]()
(2)设![]() ,
,
当![]() 时,
时,![]() ,即
,即![]()
当![]() 时,
时,![]() ,即
,即![]()
设数列![]() 的前n项和为
的前n项和为![]()
所以当![]() 时,
时, ![]()
![]()
![]()
当![]() 时,
时, ![]()
![]()
![]()
![]()
所以数列![]() 的前n项和为
的前n项和为
(3)由(1)有![]()
由![]() 有
有![]() ,所以
,所以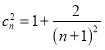
则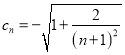 或
或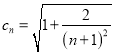
若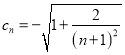 则不等式
则不等式![]() 显然成立.
显然成立.
若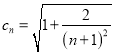 ,
,
则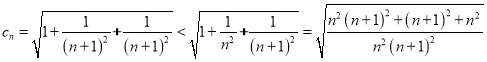
即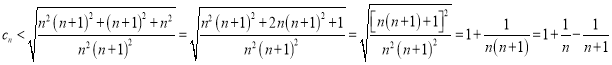 所以
所以![]()
则![]()
综上所以![]() 成立.
成立.

练习册系列答案
 同步练习强化拓展系列答案
同步练习强化拓展系列答案
相关题目
【题目】目前我国城市的空气污染越来越严重,空气质量指数![]() 一直居高不下,对人体的呼吸系统造成了严重的影响,现调查了某城市500名居民的工作场所和呼吸系统健康,得到
一直居高不下,对人体的呼吸系统造成了严重的影响,现调查了某城市500名居民的工作场所和呼吸系统健康,得到![]() 列联表如下:
列联表如下:
室外工作 | 室内工作 | 合计 | |
有呼吸系统疾病 | 150 | ||
无呼吸系统疾病 | 100 | ||
合计 | 200 |
(Ⅰ)请把![]() 列联表补充完整;
列联表补充完整;
(Ⅱ)你是否有95%的把握认为感染呼吸系统疾病与工作场所有关;
(Ⅲ)现采用分层抽样从室内工作的居民中抽取一个容量为6的样本,将该样本看成一个总体,从中随机抽取2人,求2人都有呼吸系统疾病的概率.
参考公式与临界表:![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |