题目内容
若正整数数列1,2,3,…,2n(n∈N*)中各项的最大奇数因子的和为an﹒求证:| n |
 |
| i=1 |
| 1 |
| aiai+1 |
| 3 |
| 20 |
分析:先看奇数2k+1的最大奇数因子是2k+1;形如2k(k∈N)的数的最大奇数因子是1,根据1,2,3,,2n,,2n+1中各项的最大奇数因子之和为an+1,进而表示出an+1,然后用分组求和的方法求得an的表达式,代入
,分析推断
=
<
=
,代入
即可证明原式.
| 1 |
| aiai+1 |
| 1 |
| aiai+1 |
| 9 |
| (4i+2)(4i+1+2) |
| 9 |
| 4i4i+1 |
| 9 |
| 42i+1 |
| n |
 |
| i=1 |
| 1 |
| aiai+1 |
解答:证明:显然,a1=2
下面考虑an与an+1的关系.
奇数2k+1的最大奇数因子是2k+1;形如2k(k∈N)的数的最大奇数因子是1..
由于1,2,3,,2n,,2n+1中各项的最大奇数因子之和为an+1,则an+1=1+3+5++(2n+1-1)+a'n,其中a'n是数列2,4,6,,2n+1中各项最大奇数因子之和,它等于1,2,3,,2n中各项的最大奇数因子之和.所以有an+1=1+3+5+…+(2n+1-1)+an?an+1-an=4n.
因此,an=a1+(a2-a1)+(a3-a2)++(an-an-1)=2+4+42++4n-1=
,.
从而
=
<
=
,.
故,
<
=
[1-(
)n]<
.
下面考虑an与an+1的关系.
奇数2k+1的最大奇数因子是2k+1;形如2k(k∈N)的数的最大奇数因子是1..
由于1,2,3,,2n,,2n+1中各项的最大奇数因子之和为an+1,则an+1=1+3+5++(2n+1-1)+a'n,其中a'n是数列2,4,6,,2n+1中各项最大奇数因子之和,它等于1,2,3,,2n中各项的最大奇数因子之和.所以有an+1=1+3+5+…+(2n+1-1)+an?an+1-an=4n.
因此,an=a1+(a2-a1)+(a3-a2)++(an-an-1)=2+4+42++4n-1=
| 4n+2 |
| 3 |
从而
| 1 |
| aiai+1 |
| 9 |
| (4i+2)(4i+1+2) |
| 9 |
| 4i4i+1 |
| 9 |
| 42i+1 |
故,
| n |
 |
| i=1 |
| 1 |
| aiai+1 |
| n |
 |
| i=1 |
| 9 |
| 42i+1 |
| 3 |
| 20 |
| 1 |
| 16 |
| 3 |
| 20 |
点评:本题主要考查了等差数列的 求和问题.涉及了不等式的问题,综合性强.

练习册系列答案
 智趣寒假作业云南科技出版社系列答案
智趣寒假作业云南科技出版社系列答案
相关题目
删去正整数数列
1,2,3,…中的所有完全平方数(对整数a,若存在整数b,使 ,则称a为完全平方数,如49,81等都是完全平方数),得到一个新数列,这个数列的第2005项是
,则称a为完全平方数,如49,81等都是完全平方数),得到一个新数列,这个数列的第2005项是
[
]|
A .2048 |
B .2049 |
|
C .2050 |
D .2051 |
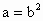 ,则称a为完全平方数,如49,81等都是完全平方数),得到一个新数列,这个数列的第2005项是
,则称a为完全平方数,如49,81等都是完全平方数),得到一个新数列,这个数列的第2005项是