Question

已知数列{a_n}，{b_n}分别是等差数列和等比数列，且a₂=b₂=2，a₄=b₄=8．

（1）求数列{a_n}，{b_n}的通项a_n，b_n．

（2）求数列{a_n}，{b_n}的前n项和S_n，T_n．

Answer 1

考点：

等比数列的前n项和；等差数列的通项公式；等差数列的前n项和；等比数列的通项公式．

专题：

等差数列与等比数列．

分析：

（1）设等差数列{a_n}的公差为d，等比数列{b_n}的公比为q，由题意可得关于首项和公差，公比的方程组，解之可得通项公式；

（2）由（1）可知通项公式，进而可得数列的前n项和公式．

解答：

解：（1）设等差数列{a_n}的公差为d，等比数列{b_n}的公比为q，

由题意可得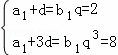，解得a₁=﹣1，d=3，或，

故由等差数列的通项公式可得a_n=﹣1+3（n﹣1）=3n﹣4，

由等比数列的求和公式可得b_n=1•2^n﹣1=2^n﹣1，或b_n=（﹣1）（﹣2）^n﹣1=﹣（﹣2）^n﹣1；

（2）由（1）可知a_n=3n﹣4，b_n=2^n﹣1，或b_n=﹣（﹣2）^n﹣1；

由等差数列的求和公式可得：S_n==，

由等差数列的求和公式可得当b_n=2^n﹣1时，T_n==2ⁿ﹣1，

当b_n=﹣（﹣2）^n﹣1时，T_n==

点评：

本题考查等差数列和等比数列的通项公式和求和公式，属中档题．