题目内容
甲、乙两人玩一种游戏 ,每次由甲、乙各出1到5根手指头,若和为偶数则算甲赢,否则算乙赢.
,每次由甲、乙各出1到5根手指头,若和为偶数则算甲赢,否则算乙赢.
(1)若以A表示“和为6”的事件,求P(A);
(2)现连玩三次,以B表示 “甲至少赢一次”的事件,C表示“乙至少赢两次”的事件,则B与C是否为互斥事件?试说明理由;
“甲至少赢一次”的事件,C表示“乙至少赢两次”的事件,则B与C是否为互斥事件?试说明理由;
(3)这种游戏规则公平吗?试说明理由.
(1)令x,y分别表示甲、乙出的手指数,则基本事件空间可表示为S={(x,y)|x∈N*,y∈N*,1≤x≤5,1≤y≤5}.
因为S中点的总数为5×5=25,
所以基本事件总数n=25.
事件A包含的基本事件为(1,5),(2,4),(3,3),(4,2),(5,1),共5个,所以P(A)= =
= .
.
(2)B与C不是互斥事件,如“甲赢一次,乙赢两次”的事件中,事件B与C是同时发生的.
(3)由(1)知,和为偶数的基本事件数为13,即甲赢的概率为 ,乙赢的概率为
,乙赢的概率为 ,所以这种游戏规则不公平.
,所以这种游戏规则不公平.

练习册系列答案
相关题目
一个容量为100的样本,其数据的分组与各组的频数如下表
| 组别 | (0,10] | (10,20] | (20,30] | (30,40] | (40,50] | (50,60] | (60,70] |
| 频数 | 12 | 13 | 24 | 15 | 16 | 13 | 7 |
则样本数据落在(10,40]上的频率为( )
A.0.13 B.0.39
C.0. 52 D.0.64
52 D.0.64
 0时,输出y的值为( )
0时,输出y的值为( )
 B.
B.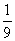
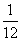 D.
D.
 则数列{ an}的公比为q为( )
则数列{ an}的公比为q为( )