题目内容
若集合A={x|y2=4x，y∈R}，
，则A∩B=（ ）A．[0，1]
B．（-2，1]
C．（-2，+∞）
D．[1，+∞）
【答案】分析：由y∈R，得
化简集合A，解分式不等式化简集合B，然后直接进行交集运算．
解答：解：由y2=4x，y∈R，所以x≥0，所以A={x|y2=4x，y∈R}={x|x≥0}；
再由
，得
，解得-2＜x≤1．
所以
={x|-2＜x≤1}，
则A∩B={x|x≥0}∩{x|-2＜x≤1}=[0，1]．
故选A．
点评：本题考查了分式不等式的解法，考查了交集及其运算，是基础的计算题．
化简集合A，解分式不等式化简集合B，然后直接进行交集运算．解答：解：由y2=4x，y∈R，所以x≥0，所以A={x|y2=4x，y∈R}={x|x≥0}；
再由
，得，解得-2＜x≤1．所以
={x|-2＜x≤1}，则A∩B={x|x≥0}∩{x|-2＜x≤1}=[0，1]．
故选A．
点评：本题考查了分式不等式的解法，考查了交集及其运算，是基础的计算题．
练习册系列答案
激活思维智能训练课时导学练系列答案
相关题目
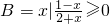，则A∩B=
，则A∩B=（ ）