题目内容
若集合A={x|y2=4x,y∈R},B={x|
≥0},则A∩B=( )
| 1-x |
| 2+x |
| A.[0,1] | B.(-2,1] | C.(-2,+∞) | D.[1,+∞) |
由y2=4x,y∈R,所以x≥0,所以A={x|y2=4x,y∈R}={x|x≥0};
再由
≥0,得
,解得-2<x≤1.
所以B={x|
≥0}={x|-2<x≤1},
则A∩B={x|x≥0}∩{x|-2<x≤1}=[0,1].
故选A.
再由
| 1-x |
| 2+x |
|
所以B={x|
| 1-x |
| 2+x |
则A∩B={x|x≥0}∩{x|-2<x≤1}=[0,1].
故选A.

练习册系列答案
相关题目
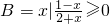 ,则A∩B=
,则A∩B= ,则A∩B=( )
,则A∩B=( ) ,则A∩B=( )
,则A∩B=( )